树与类树

发表于 更新于 分类于 阅读次数： 本文字数： 31k 阅读时长 ≈ 29 分钟
引言：树与类似树的数据结构，做一个总篇（BST、AVL、红黑树、线段树、TriE、并查集、堆）

树

本文的内容来自于自己的其他博客（大约在2020年写的），最近正好在复习数据结构相关内容，此处做一个树与类树的相关整理。

二叉树

树的基本结构，不过多叙述：

  • 具有天然的递归结构：每个结点的左、右子树都是二叉树

二叉树

  • 满二叉树：除了叶子结点外，每个结点都有两个孩子

  • 完全二叉树：除最后一层，每个节点都有两个孩子，而且最后一层的孩子尽量靠左

    完全二叉树

BST

  • 首先是一棵二叉树
  • 独有的特点：每一个节点的值
    • 大于左子树所有结点的值
    • 小于右子树所有结点的值
  • 每一棵子树也是二分搜索树

注意：存储的元素必须具有可比较性，存储一个int类的数据，当然可以比较大小，但是存储一个学生类、车类等实体类，我们必须规定它的比较方式，比如学生可以按年龄比较等等

二分搜索树代码

Java实现一个BST树

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
//泛型必须满足可比较性，所以继承了Comparable接口
public class BinarySearchTree<E extends Comparable<E>> {
    private class Node {
        public E e;
        public Node left, right;
        public Node(E e) {
            this.e = e;
            left = null;
            right = null;
        }
    }

    private Node root;
    private int size;
    public BinarySearchTree() {
        root = null;
        size = 0;
    }
    public int size() {
        return size;
    }
    public boolean isEmpty() {
        return size == 0;
    }

    public void add(E e) {
        root = add(root, e);
    }

    /**
     * 递归插入
     */
    private Node add(Node node, E e) {
        if (node == null) {
            size++;
            return new Node(e);
        }
        if (e.compareTo(node.e) > 0) {
            node.right = add(node.right, e);
        } else if (e.compareTo(node.e) < 0) {
            node.left = add(node.left, e);
        }
        return node;
    }

    public boolean contains(E e) {
        return contains(root, e);
    }
    /**
     * 递归
     */
    public boolean contains(Node node, E e) {
        if (node == null) {
            return false;
        }
        if (node.e.compareTo(e) == 0) {
            return true;
        } else if (node.e.compareTo(e) > 0) {
            return contains(node.left, e);
        } else {
            return contains(node.right, e);
        }
    }

    /**
     * 前序遍历二叉搜索树：根 -> 左 -> 右
     */
    public void preOrder() {
        preOrder(root);
    }

    private void preOrder(Node node) {
        if (node == null) {
            return;
        }
        System.out.println(node.e);
        preOrder(node.left);
        preOrder(node.right);
    }

    /**
     * 中序遍历二叉搜索树：左 -> 根 -> 右
     */
    public void inOrder() {
        inOrder(root);
    }

    private void inOrder(Node node) {
        if (node == null) {
            return;
        }
        inOrder(node.left);
        System.out.println(node.e);
        inOrder(node.right);
    }

    /**
     * 二叉搜索树的后序遍历：左 -> 右 -> 根
     */
    public void postOrder() {
        postOrder(root);
    }

    private void postOrder(Node node) {
        if (node == null) {
            return;
        }
        postOrder(node.left);
        postOrder(node.right);
        System.out.println(node.e);
    }




    /**
     * 返回以node为根的二分搜索树的最小值所在的节点
     * @return
     */
    private Node minimum(Node node){
        if(node.left == null){
            return node;
        }
        return minimum(node.left);
    }

    /**
     * 返回以node为根的二分搜索树的最大值所在的节点
     * @return
     */
    private Node maximum(Node node){
        if(node.right == null){
            return node;
        }
        return minimum(node.right);
    }

    /**
     * 寻找最小值
     * @return
     */
    public E minimum(){
        if(size==0){
            throw new IllegalArgumentException("BST is empty!");
        }
        return minimum(root).e;
    }

    /**
     * 寻找最大值
     * @return
     */
    public E maximum(){
        if(size==0){
            throw new IllegalArgumentException("BST is empty!");
        }
        return maximum(root).e;
    }

    /**
     * 删除最小值
     * @return
     */
    public E removeMin(){
        E ret = minimum();
        root = removeMin(root);
        return ret;
    }

    /**
     * 删除以node为根的最小结点
     * @param node
     * @return 删除节点后新的二分搜索树的根
     */
    private Node removeMin(Node node) {
        if(node.left ==null){
            Node rightNode = node.right;
            node.right = null;
            size--;
            return rightNode;
        }
        node.left = removeMin(node.left);
        return node;
    }

    /**
     * 删除最大值
     * @return
     */
    public E removeMax(){
        E ret = maximum();
        root = removeMax(root);
        return ret;
    }

    private Node removeMax(Node node) {
        if(node.right ==null){
            Node leftNode = node.left;
            node.left = null;
            size--;
            return leftNode;
        }
        node.right = removeMax(node.right);
        return node;
    }

    /**
     * 删除任意结点：1962年Hibbard提出的-Hibbard Deletion
     * @param e
     * @return
     */
    public void remove(E e){
        root = remove(root, e);
    }

    /**
     * 删除以node为根的二分搜索树中值为 e 的结点
     * @param node
     * @param e
     * @return
     */
    private Node remove(Node node, E e){
        if(node == null){
            return null;
        }
        if(e.compareTo(node.e) < 0){
            node.left = remove(node.left, e);
            return node;
        }else if(e.compareTo(node.e) > 0){
            node.right = remove(node.right, e);
            return node;
        }else{ // e 等于 node.e
            if(node.left == null){
                Node rightNode = node.right;
                node.right = null;
                size --;
                return rightNode;
            }
            if(node.left == null){
                Node leftNode = node.left;
                node.left = null;
                size --;
                return leftNode;
            }
            // 左右结点的左右子树均不为空
            // 找 “最近” 的结点，这里找了被删除结点的后驱结点，其实也可以选择前驱
            Node successor = minimum(node.right);
            successor.right = removeMin(node.right);
            successor.left = node.left;
            // 与不再有关系，将node左右结点置为空
            node.left = node.right = null;
            return successor;
        }
    }
}

DFS使用栈

迭代的方式进行前序遍历（对于中序遍历可能会难一点，见LeetCode 中序遍历 题目）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
/**
     * 前序遍历二叉搜索树：非递归（深度优先遍历）
     * 使用栈来辅助存储
     * 要点：先将右孩子压入栈，然后将左孩子压入栈，因为出栈时是先进后出，所以前序遍历要先压入右孩子
     */
public void preOrderNR() {
    Stack<Node> stack = new Stack<Node>();
    stack.push(root);
    while (!stack.isEmpty()){
        Node cur = stack.pop();
        System.out.println(cur.e);
        if(cur.right!=null) {
            // 先压入右孩子
            stack.push(cur.right);
        }
        if(cur.left!=null){
            stack.push(cur.left);
        }
    }
}

BFS使用队列

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
/**
 * 二叉搜索树的层序遍历（广度优先遍历）
 * 使用队列来辅助记录孩子节点
 */
public void levelOrder(){
    Queue<Node> queue = new LinkedList<>();
    queue.add(root);
    while (!queue.isEmpty()){
        Node cur = queue.remove();
        System.out.println(cur.e);
        if(cur.left!=null){
            queue.add(cur.left);
        }
        if(cur.right!=null){
            queue.add(cur.right);
        }
    }
}

前继与后继节点

1962年Hibbard提出的-Hibbard Deletion

删除任意结点操作中，删除一个任意结点的值，关键在于要糅合被删除结点的孩子结点，关键是要找到被删除结点的“最近”的节点，如图，绿色的结点就是被删除结点的最近的结点

后继节点

所以我们要做的事情就是用这个绿色的结点替换掉蓝色的结点，就可以了

(你可能发现了，其实也可以找53这个结点)

实际使用中：

  • 中序遍历使用最广，因为前序遍历得到的是一个有序的串
  • 后序遍历的思想可以使用在内存的释放过程中
  • 前序遍历其实也叫作深度优先遍历
  • 层序遍历也叫作广度优先遍历

注意：当存入的数据是一个有序的数据时，我们的二叉搜索树会退化成一个链表，为了解决这个问题，我们就要实现平衡二叉树（以后我们会说到平衡二叉树）

AVL

平衡二叉树：任意节点的左子树和右子树的高度差不能超过1

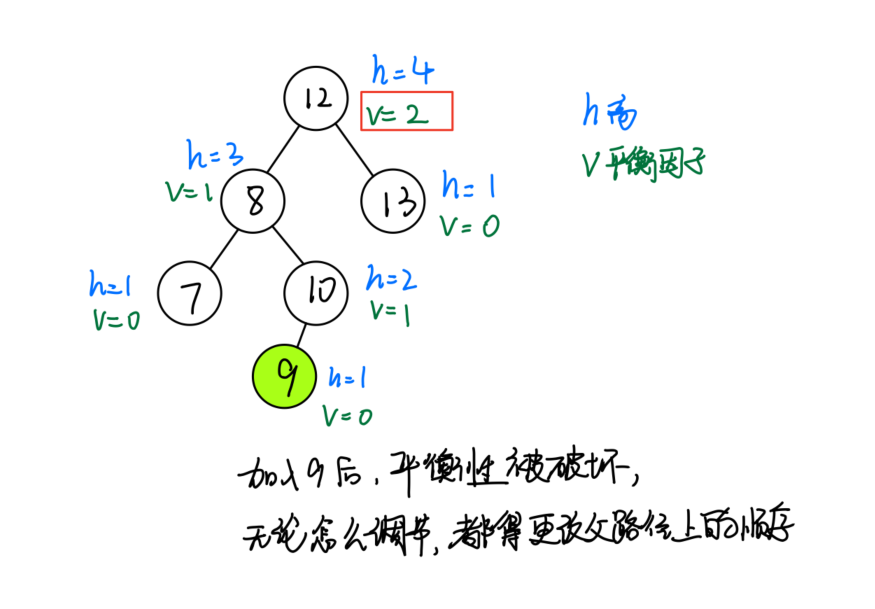
平衡因子

AVL通过平衡因子判断当前节点是否平衡，即它的左右子树差超过1的时候，认为不平衡

avl树的平衡因子

树上黑色的数字代表该节点的高度：

  • 例如2那个叶子节点，它的高度是1
  • 例如8那个节点，它的左子树高度是3，右子树高度是1，那么他的高度就是较大的那个树的高度再加1，就是4

树上的蓝色数字代表这个结点的平衡因子：

  • 例如2那个叶子结点，它的左右孩子都是null，所以它的平衡因子是0 - 0 = 0
  • 例如8那个叶子结点，它的左子树高度为3，右子树高度为1，所以它的平衡因子是3 - 1 = 2，超过了1，所以该树从这个结点开始不再平衡

平衡被破坏

当我们从一个根节点开始不断插入值的时候，这棵树会不断的生长，如果在插入一个值的时候，平衡被破坏了，那么不管如何，将这颗树改为平衡状态一定是在这个叶子节点的父节点路径上

AVL平衡被插入破坏

左旋与右旋

一种最早的也是最经典的平衡二叉树，由G.M.Adelson-Velsky和E.M.Landis两位俄罗斯的科学家找出了 左旋和右旋 两种操作来实现树的平衡。

对于平衡二叉树，有两种不平衡的状况（如图）：

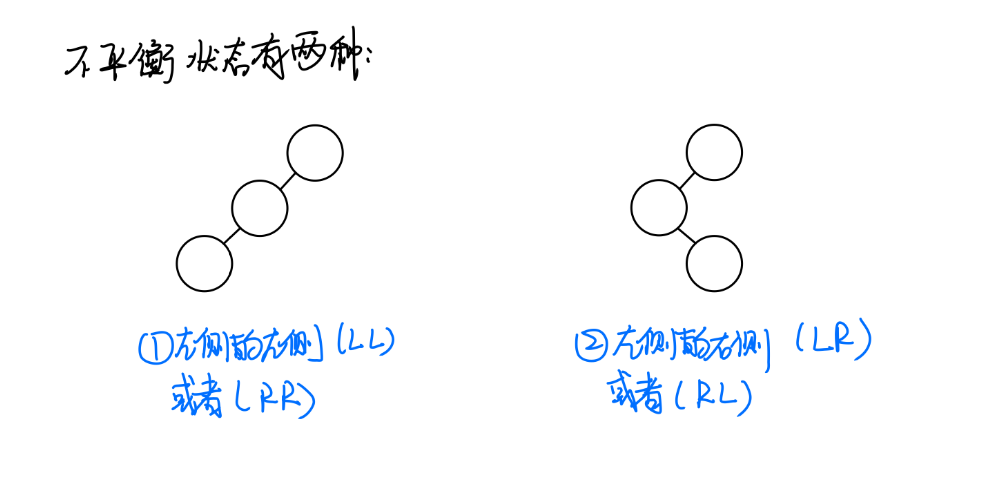
不平衡状态

以上的两种状况其实可以分为两类：

  • LL 与 RR
  • LR 与 RL

我们先来看右旋（同理可以得到左旋的代码）如图：

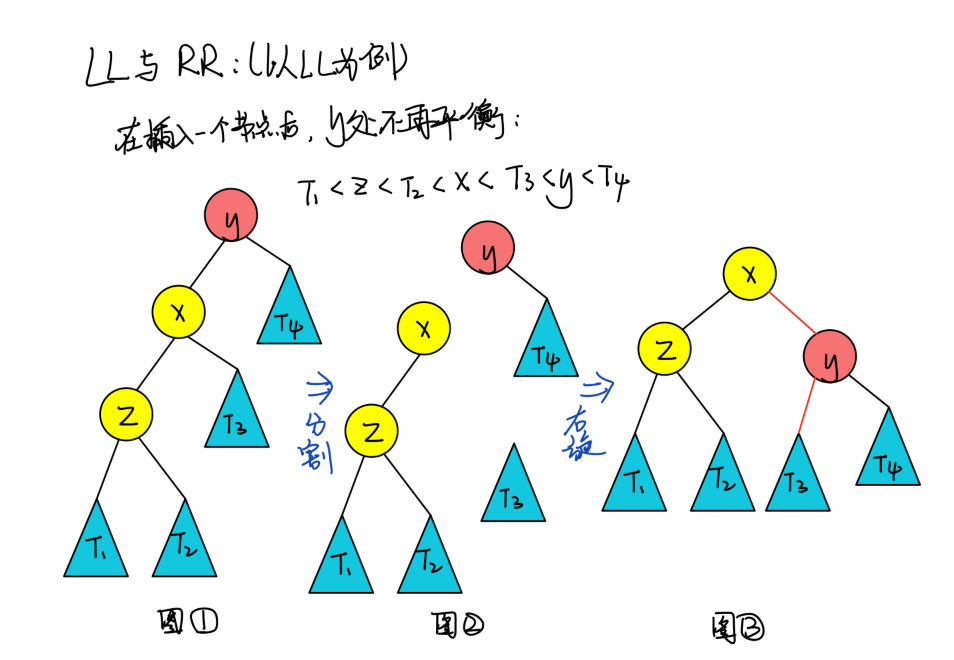
LL与RR

在右旋完成后，我们需要去更新height（平衡因子）两个值，但是留心观察我们会发现，其实只需要更新x和y，而且要先更新y再更新x（因为对于T3来说根本没有发生变化，先更新y的原因是因为更新x需要y的值，所以要先更新y）

右旋代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
    // 对节点y进行向右旋转操作，返回旋转后新的根节点x
    //        y                              x
    //       / \                           /   \
    //      x   T4     向右旋转 (y)        z     y
    //     / \       - - - - - - - ->    / \   / \
    //    z   T3                       T1  T2 T3 T4
    //   / \
    // T1   T2
private Node rightRotate(Node y) {
    Node x = y.left;
    Node T3 = x.right;

    // 向右旋转过程
    x.right = y;
    y.left = T3;

    // 更新height
    y.height = Math.max(getHeight(y.left), getHeight(y.right)) + 1;
    x.height = Math.max(getHeight(x.left), getHeight(x.right)) + 1;

    return x;
}

对于LR与RL这种情况，只需先转换为LL与RR情况，在做改变即可：

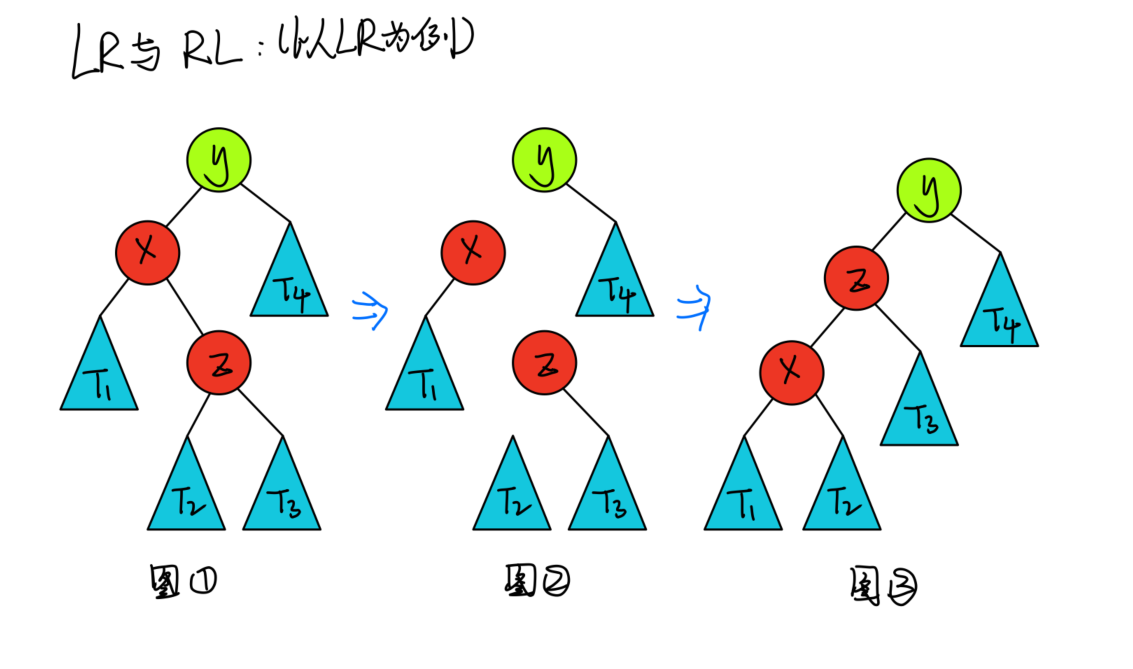
LR与RL

完整代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
294
295
296
297
298
299
300
301
302
public class AVLTree<K extends Comparable<K>,V> {
    private class Node {
        public K key;
        public V value;
        public Node left, right;
        public int height; // 当前所处高度值

        public Node(K key, V value) {
            this.key = key;
            this.value = value;
            left = null;
            right = null;
            height = 1; //默认高度为1
        }
    }

    private Node root;
    private int size;

    public AVLTree() {
        root = null;
        size = 0;
    }

    // * 获得结点的高度
    private int getHeight(Node node){
        if(node==null) {
            return 0;
        }
        return node.height;
    }
    // * 计算结点的平衡因子

    private int getBalanceFactor(Node node){
        if(node == null) {
            return 0;
        }
        return getHeight(node.left) - getHeight(node.right);
    }

    public void add(K key, V value) {
        root = add(root, key, value);
    }

    // 判断该二叉树是否是一个平衡二叉树
    public boolean isBalanced(){
        return isBalanced(root);
    }
    public boolean isBalanced(Node node){
        if(node == null) {
            return true;
        }
        int balanceFactor = getBalanceFactor(node);
        if(Math.abs(balanceFactor) > 1)
            return false;
        return isBalanced(node.left) && isBalanced(node.right);
    }


    // * 每次增加结点改变高度值
    private Node add(Node node, K key, V value) {
        if (node == null) {
            size++;
            return new Node(key, value);
        }
        
        if(key.compareTo(node.key) < 0) {
            node.left = add(node.left, key, value);
        } else if(key.compareTo(node.key) > 0) {
            node.right = add(node.right, key, value);
        } else // key.compareTo(node.key) == 0
        {
            node.value = value;
        }

        // 对当前的node值更新它的height：它的高度是左右子树更高那个加1
        node.height = 1 + Math.max(getHeight(node.left),getHeight(node.right));

        // 计算结点的平衡因子
        int balanceFactor = getBalanceFactor(node);
        // 如果平衡因子(有可能为负数)超过了1 ，那么我们就需要进行自平衡了
        // 如果不平衡，那么判断这个结点的两个孩子：如果左孩子平衡值大于等于0，那么需要右旋；如果右孩子平衡值大于等于0，那么需要左旋
        // LL
        if (balanceFactor > 1 && getBalanceFactor(node.left) >= 0) {
            return rightRotate(node);
        }
        // RR
        if (balanceFactor < -1 && getBalanceFactor(node.right) <= 0) {
            return leftRotate(node);
        }
        // LR
        if (balanceFactor > 1 && getBalanceFactor(node.left) < 0) {
            node.left = leftRotate(node.left);
            return rightRotate(node);
        }
        // RL
        if (balanceFactor < -1 && getBalanceFactor(node.right) > 0) {
            node.right = rightRotate(node.right);
            return leftRotate(node);
        }
        return node;
    }

    // 对节点y进行向右旋转操作，返回旋转后新的根节点x
    //        y                              x
    //       / \                           /   \
    //      x   T4     向右旋转 (y)        z     y
    //     / \       - - - - - - - ->    / \   / \
    //    z   T3                       T1  T2 T3 T4
    //   / \
    // T1   T2
    private Node rightRotate(Node y) {
        Node x = y.left;
        Node T3 = x.right;

        // 向右旋转过程
        x.right = y;
        y.left = T3;

        // 更新height
        y.height = Math.max(getHeight(y.left), getHeight(y.right)) + 1;
        x.height = Math.max(getHeight(x.left), getHeight(x.right)) + 1;

        return x;
    }

    // 对节点y进行向左旋转操作，返回旋转后新的根节点x
    //    y                             x
    //  /  \                          /   \
    // T1   x      向左旋转 (y)       y     z
    //     / \   - - - - - - - ->   / \   / \
    //   T2  z                     T1 T2 T3 T4
    //      / \
    //     T3 T4
    private Node leftRotate(Node y) {
        Node x = y.right;
        Node T2 = x.left;

        // 向左旋转过程
        x.left = y;
        y.right = T2;

        // 更新height
        y.height = Math.max(getHeight(y.left), getHeight(y.right)) + 1;
        x.height = Math.max(getHeight(x.left), getHeight(x.right)) + 1;

        return x;
    }


    private Node removeMin(Node node) {
        if (node.left == null) {
            Node rightNode = node.right;
            node.right = null;
            size--;
            return rightNode;
        }
        node.left = removeMin(node.left);
        return node;
    }

    /**
     * 寻找最小值
     */
    public V minimum() {
        if (size == 0) {
            throw new IllegalArgumentException("BST is empty!");
        }
        return minimum(root).value;
    }

    /**
     * 返回以node为根的二分搜索树的最小值所在的节点
     *
     * @return
     */
    private Node minimum(Node node) {
        if (node.left == null) {
            return node;
        }
        return minimum(node.left);
    }

    public V remove(K key) {
        Node node = getNode(root, key);
        if (node != null) {
            root = remove(root, key);
        }

        return null;
    }

    private Node remove(Node node, K key){
        if( node == null ) {
            return null;
        }
        Node retNode;
        if( key.compareTo(node.key) < 0 ){
            node.left = remove(node.left , key);
            // return node;
            retNode = node;
        }
        else if(key.compareTo(node.key) > 0 ){
            node.right = remove(node.right, key);
            // return node;
            retNode = node;
        }
        else{   // key.compareTo(node.key) == 0
            // 待删除节点左子树为空的情况
            if(node.left == null){
                Node rightNode = node.right;
                node.right = null;
                size --;
                // return rightNode;
                retNode = rightNode;
            }
            // 待删除节点右子树为空的情况
            else if(node.right == null){
                Node leftNode = node.left;
                node.left = null;
                size --;
                // return leftNode;
                retNode = leftNode;
            }
            // 待删除节点左右子树均不为空的情况
            else{
                // 找到比待删除节点大的最小节点, 即待删除节点右子树的最小节点
                // 用这个节点顶替待删除节点的位置
                Node successor = minimum(node.right);
                //successor.right = removeMin(node.right);
                successor.right = remove(node.right, successor.key);
                successor.left = node.left;

                node.left = node.right = null;

                // return successor;
                retNode = successor;
            }
        }
        if(retNode == null) {
            return null;
        }
        // 更新height
        retNode.height = 1 + Math.max(getHeight(retNode.left), getHeight(retNode.right));
        // 计算平衡因子
        int balanceFactor = getBalanceFactor(retNode);
        // 平衡维护
        // LL
        if (balanceFactor > 1 && getBalanceFactor(retNode.left) >= 0)
            return rightRotate(retNode);
        // RR
        if (balanceFactor < -1 && getBalanceFactor(retNode.right) <= 0)
            return leftRotate(retNode);
        // LR
        if (balanceFactor > 1 && getBalanceFactor(retNode.left) < 0) {
            retNode.left = leftRotate(retNode.left);
            return rightRotate(retNode);
        }
        // RL
        if (balanceFactor < -1 && getBalanceFactor(retNode.right) > 0) {
            retNode.right = rightRotate(retNode.right);
            return leftRotate(retNode);
        }
        return retNode;
    }

    // 返回以node为根节点的二分搜索树中，key所在的节点
    private Node getNode(Node node, K key){
        if(node == null) {
            return null;
        }
        if(key.equals(node.key)) {
            return node;
        } else if(key.compareTo(node.key) < 0) {
            return getNode(node.left, key);
        } else // if(key.compareTo(node.key) > 0)
        {
            return getNode(node.right, key);
        }
    }
    
    public boolean contains(K key) {
        return getNode(root, key) != null;
    }
    public V get(K key) {
        Node node = getNode(root, key);
        return node == null ? null : node.value;
    }
    public void set(K key, V newValue){
        Node node = getNode(root, key);
        if(node == null) {
            throw new IllegalArgumentException(key + " doesn't exist!");
        }
        node.value = newValue;
    }
    public int getSize() {
        return size;
    }
    public boolean isEmpty() {
        return size == 0;
    }
}

2-3树

在了解红黑树之前，要先学习一下2-3树

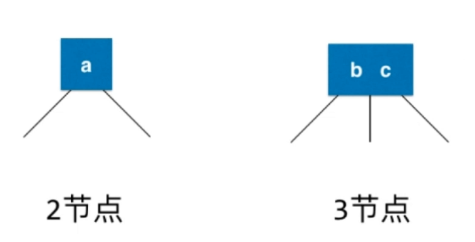
2-3树：满足二分搜索树的性质，但不是二叉树。

2-3树就是每个节点有2个或者3个孩子的树

2-3树

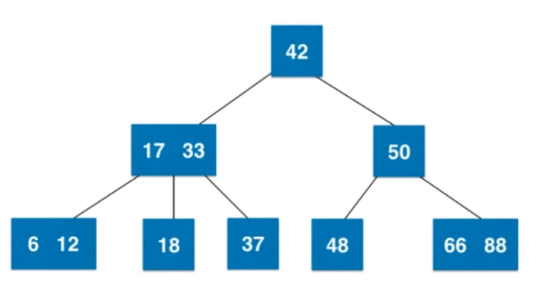
例如这就是一棵2-3树：

2-3树

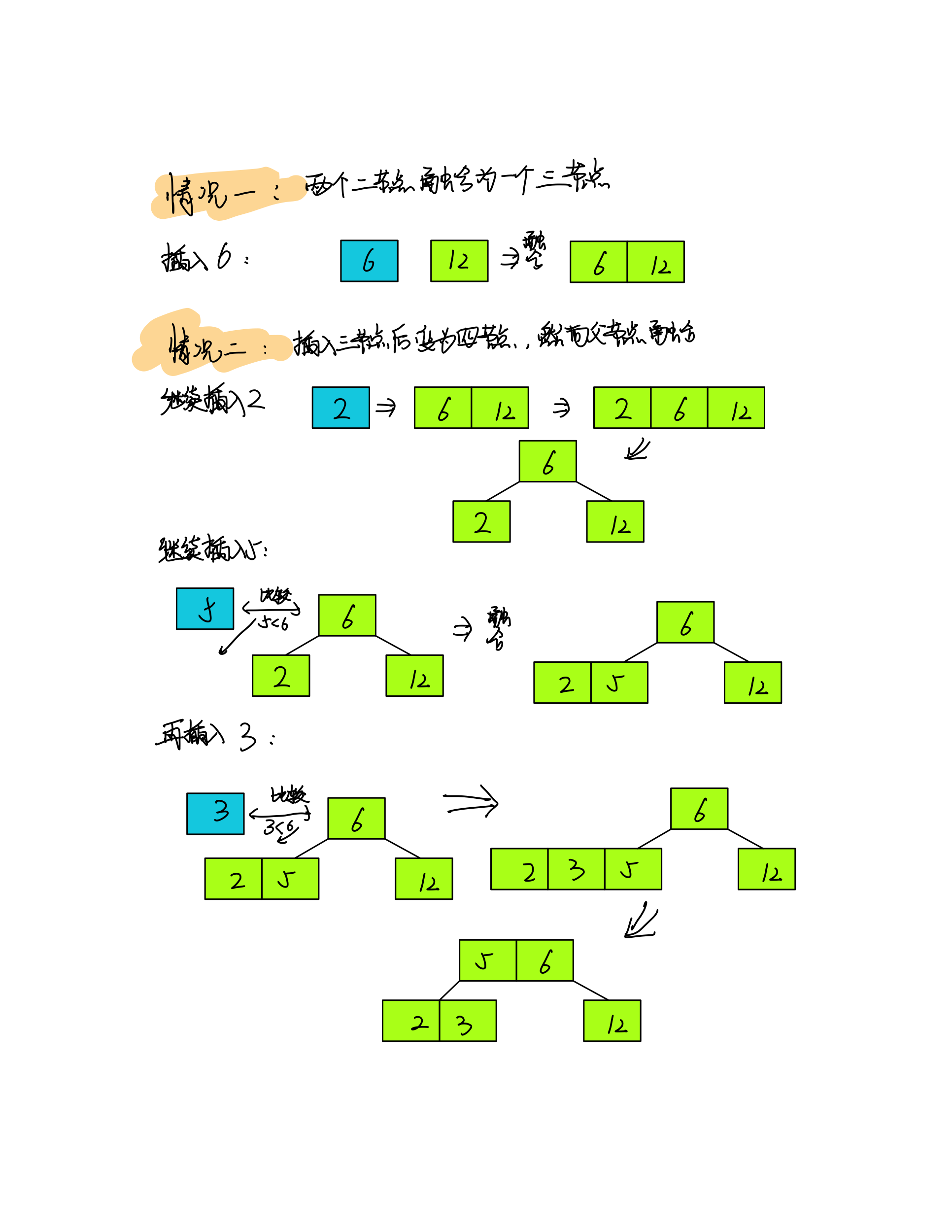
重要的性质：2-3树是一棵绝对平衡（从根节点到任意节点的路径一定是相同的）的树

绝对平衡

如图：2-3树是一棵可以保持绝对平衡的树

绝对平衡

红黑树

2-3树与红黑树的等价

在理解2-3树是什么之后，理解红黑树就不会太难了。2-3树与红黑树之间的关系如图：

2-3节点与红黑节点的对应关系

由此我们再来看红黑树的性质：

红黑树就是这样的树：

  1. 每个节点是红色或者黑色
  2. 根节点是黑色
  3. 叶子节点是黑色
  4. 如果一个节点是红色的，那么他的孩子节点都是黑色的
    • 如果一个红节点的孩子有一个是红色的，就出现四节点了，就不是我们所说的2-3树了
  5. 从任意一个节点到叶子节点，经过的黑色节点是一样的（黑平衡）
    • 如同2-3树，是一棵绝对平衡的树

添加元素

红黑树只会添加红节点，以这个为前提，我们来看

红黑树添加元素

红黑树添加节点

左旋、右旋、颜色翻转

现在有一个二节点要加入到一个三节点上：

  • 加在了黑节点的右子树上：直接颜色翻转
  • 加在了红节点的左子树上：先右旋，后颜色翻转
  • 加在了红节点的右子树上：先左旋，再右旋，再颜色翻转

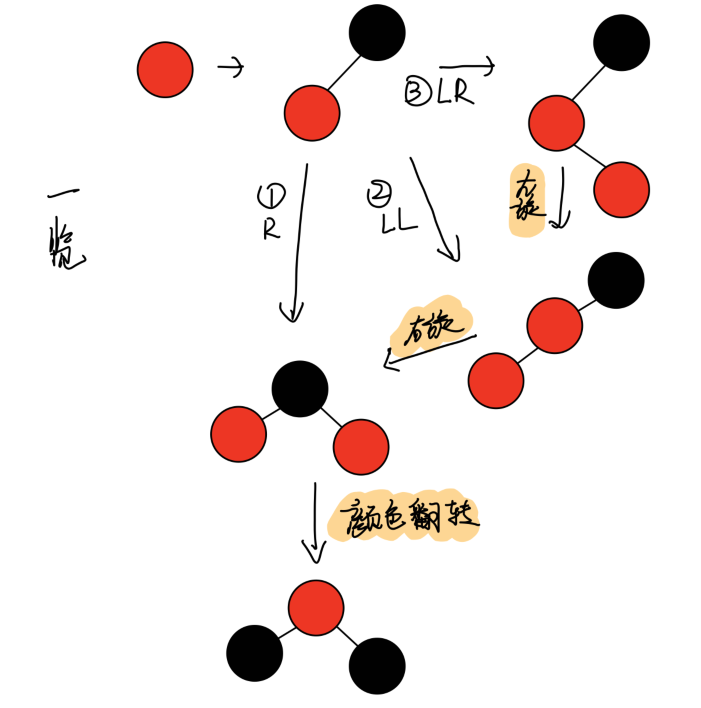
左旋右旋颜色翻转

完整代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
public class RBTree<K extends Comparable<K>, V> {

    // * 表示红色与黑色
    private static final boolean RED = true;
    private static final boolean BLACK = false;

    private class Node{
        public K key;
        public V value;
        public Node left, right;
        public boolean color;

        public Node(K key, V value){
            this.key = key;
            this.value = value;
            left = null;
            right = null;
            color = RED;    //* 只插入黑色节点
        }
    }

    private Node root;
    private int size;

    public RBTree(){
        root = null;
        size = 0;
    }

    public int getSize(){
        return size;
    }

    public boolean isEmpty(){
        return size == 0;
    }

    // * 判断节点node的颜色
    private boolean isRed(Node node){
        // * 为null代表叶子结点，叶子节点都是黑色
        if(node == null) {
            return BLACK;
        }
        return node.color;
    }

    //   node                     x
    //  /   \     左旋转         /  \
    // T1   x   --------->   node   T3
    //     / \              /   \
    //    T2 T3            T1   T2
    private Node leftRotate(Node node){
        Node x = node.right;
        // 左旋转
        node.right = x.left;
        x.left = node;
        // 改变颜色
        x.color = node.color;   // 新的根节点继承原本根节点的颜色
        node.color = RED;       // 左孩子变为红色
        return x;

    }
    //   node                     x
    //  /   \     右旋转         /  \
    //  x   T2   --------->     y   node
    // / \                           / \
    //y   T1                       T1   T2
    private Node rightRotate(Node node){
        Node x = node.left;
        // 右旋转
        node.left = x.right;
        x.right = node;
        // 维持节点颜色
        x.color = node.color;
        node.color = RED;
        return x;
    }

    // * 颜色翻转
    private void filpColors(Node node){
        node.color = RED;
        node.left.color = BLACK;
        node.right.color = BLACK;
    }

    // 向红黑树中添加新的元素(key, value)
    public void add(K key, V value){
        root = add(root, key, value);
        root.color = BLACK; // 完成后的根节点必须为黑色节点
    }

    // 向以node为根的红黑树中插入元素(key, value)，递归算法
    // 返回插入新节点后红黑树的根
    private Node add(Node node, K key, V value){

        if(node == null){
            size ++;
            return new Node(key, value); // 默认插入红色节点
        }
        if(key.compareTo(node.key) < 0) {
            node.left = add(node.left, key, value);
        } else if(key.compareTo(node.key) > 0) {
            node.right = add(node.right, key, value);
        } else // key.compareTo(node.key) == 0
        {
            node.value = value;
        }
        // 左黑右红 -> 左旋
        if(isRed(node.right) && !isRed(node.left)){
            node =leftRotate(node);
        }
        // LL都为红
        if(isRed(node.left) && isRed(node.left.left)){
            node = rightRotate(node);
        }
        // 左右为红
        if(isRed(node.left) && isRed(node.right)){
            filpColors(node);
        }

        return node;
    }

    // 返回以node为根节点的二分搜索树中，key所在的节点
    private Node getNode(Node node, K key){

        if(node == null) {
            return null;
        }

        if(key.equals(node.key)) {
            return node;
        } else if(key.compareTo(node.key) < 0) {
            return getNode(node.left, key);
        } else // if(key.compareTo(node.key) > 0)
        {
            return getNode(node.right, key);
        }
    }

    public boolean contains(K key){
        return getNode(root, key) != null;
    }

    public V get(K key){

        Node node = getNode(root, key);
        return node == null ? null : node.value;
    }

    public void set(K key, V newValue){
        Node node = getNode(root, key);
        if(node == null) {
            throw new IllegalArgumentException(key + " doesn't exist!");
        }

        node.value = newValue;
    }

    // 返回以node为根的二分搜索树的最小值所在的节点
    private Node minimum(Node node){
        if(node.left == null) {
            return node;
        }
        return minimum(node.left);
    }

    // 删除掉以node为根的二分搜索树中的最小节点
    // 返回删除节点后新的二分搜索树的根
    private Node removeMin(Node node){

        if(node.left == null){
            Node rightNode = node.right;
            node.right = null;
            size --;
            return rightNode;
        }

        node.left = removeMin(node.left);
        return node;
    }
}

对比AVL

红黑树不是完美的平衡树，只是实现了黑平衡，牺牲了平衡性，换来了插入与查询速度的均衡态

  • 对于查询较多的情况，AVL树较好（红黑树牺牲了平衡性，达到了2logn）的高度
  • 红黑树的统计性能更好（综合增删查改所有操作）

Trie

一个便于搜索的多叉树。我们学习了树结构实现映射，它的时间复杂度是O(log n)，如果有两百万个条目，大约会花费20，但是Tire查询每个条目的时间复杂度和字典中一共有多少条目无关，取决于查询单词的长度O(w)

一棵Trie就像是这样

Trie

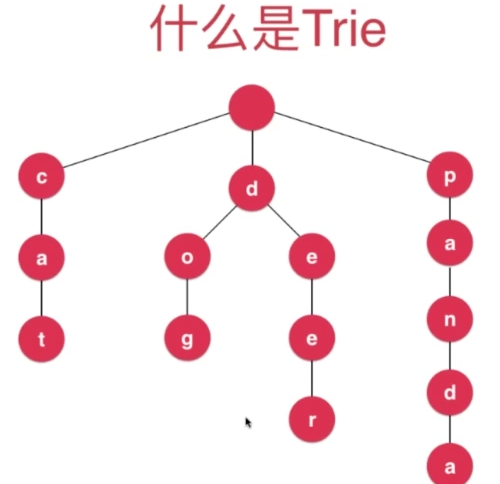
字典树结构

那么这样的一棵树，它的节点是如何定义的？

1
2
3
4
5
6
7
8
9
class Node{
    char c;
    Node next[];

    public Node(char c) {
        this.c = c;
        this.next = new Node[26];
    }
}

假如我们的业务是实现单词的存储，那么应该就是这样，每一个结点可以存储26个字母。

但是假如我们的业务是存储网址信息等等，我们会扩展到更多更多，所以我们可以使用一个Map集合来充当这里的数据

1
2
3
class Node{
    Map<Character, Node> next;
}

但是，如果要存储单词的话，我们会遇到一个问题，就是假设存储cat和category，两个词前面都是cat，那么我们如何存储呢？

我们可以再给Node加一个字段，就是isWord

1
2
3
4
class Node{
    boolean isWord;
    Map<Character, Node> next;
}

完整代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
public class Trie{
    private class Node{
        boolean isWord;
        Map<Character, Node> next;

        public Node(boolean isWord) {
            this.isWord = isWord;
            this.next = new TreeMap<>();
        }
        public Node(){
            this(false);
        }
    }
    private Node root;
    private int size;

    public Trie(){
        root = new Node();
        size =0;
    }
    public int getSize(){
        return size;
    }
    public void add(String word){
        Node cur = root;
        char[] chars = word.toCharArray();
        for (int i = 0; i < chars.length; i++) {
            if(cur.next.get(chars[i]) == null){
                cur.next.put(chars[i], new Node());
            }
            cur = cur.next.get(chars[i]);
        }
        // 如果之前这不是一个单词
        if(!cur.isWord){
            cur.isWord = true;
            size ++;
        }
    }
    // 查询是否有一个单词
    public boolean contains(String word){
        Node cur = root;
        char[] chars = word.toCharArray();
        for (int i = 0; i < chars.length; i++) {
            if(cur.next.get(chars[i]) == null){
                return false;
            }
            cur = cur.next.get(chars[i]);
        }
        return cur.isWord;
    }

    /** 查询是否在Tire中以prefix为前缀的单词
     */
    public boolean isPrefix(String prefix){
        Node cur = root;
        char[] chars = prefix.toCharArray();
        for (int i = 0; i < chars.length; i++) {
            if(cur.next.get(chars[i]) == null){
                return false;
            }
            cur = cur.next.get(chars[i]);
        }
        return true;
    }
}

线段树

区间染色问题

线段树也叫区间树(Segment Tree)，有些问题我们关注的是一个区间

例如区间染色问题

区间染色问题：有一个数组区间[0~N]区间，每次操作，我们将其一段染为一种颜色（颜色可以覆盖）

  1. 经过m次操作后，我们能看到多少种颜色？
  2. m次操作后，我们能在[i , j]区间内看到多少种颜色？

审题我们可以知道主要有两种操作：

  1. 染色操作
  2. 查询操作

自然而然我们会选择遍历数组，但是这样的话，染色操作和查询操作都需要O(N)的复杂度

再比如计算机经常会有的区间查询操作，我们可能也要统计一个区间的最大值，最小值，区间和等等信息。再比如，你想统计一下2020年你们项目中消费最高的用户，消费最少的用户，学习时间最长的用户。如果我们使用线段树，我们进行这种的操作都可以实现在O(log N)之内

那么什么是线段树？

和普通的树唯一的区别，就是每个节点存放的数据是一个区间

线段树

线段树特点：

  • 是一棵平衡二叉树（任意节点的最大深度和最小深度的差最大为1）
  • 可以使用数组来表示（虽然叶子结点不会分布在同一层，但是我们可以把不存在的叶子结点当做空来处理）
  • 一个n个节点的线段树需要开辟4n个空间

为什么一个n个节点的线段树需要4n个空间？

对于一颗平衡二叉树来说，第一层有2^0个节点，一直到第h层，有2^h个节点。整棵树总共有着2^(h+1）-1个节点，对比最后一层和全部节点数我们会有这样的感觉，几乎最后一层的节点数就和整棵树的大小是一样的，而线段树基本就是使用最后一层来存储元素。

有了上述的观念，我们再来看这个问题。因为我们要以满二叉树的标准来存储元素，假设有n个节点，而n=2^h，我们只需要使用2n个存储空间即可。，但是如果再多一个节点，我们就需要再开辟一行空间，也就是再来一行，需要使用4n个空间

完整代码

（无增添操作，线段树的优势在于实现更新和查询操作）

这里我们使用一个接口，来表示两个元素之间的相互操作。例如相加操作、相减操作等等一系列甚至是复杂的业务操作

1
2
3
public interface Merger<E> {
    E merge(E a, E b);
}

具体代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
public class SegmentTree<E> {
    private E[] data;
    private E[] tree;
    // 根据具体业务决定
    private Merger<E> merger;

    public SegmentTree(E[] arr, Merger<E> merger) {
        this.merger = merger;
        data = (E[]) new Object[arr.length];
        for (int i = 0; i < arr.length; i++) {
            data[i] = arr[i];
        }
        tree = (E[]) new Object[4 * arr.length];
        buildSegmentTree(0, 0, arr.length - 1);
    }

    /** 创建线段树
      */
    private void buildSegmentTree(int treeIndex, int l, int r) {
        // 如果只有一个元素
        if (l == r) {
            tree[treeIndex] = data[l];
            return;
        }
        // 注意这里的范围，可以写为 (r+l)/2，但是r+l可能会出现整型溢出的问题
        // 所以我们这样写 l+(r-l)/2
        int mid = l + (r - l) / 2;
        buildSegmentTree(leftChild(treeIndex), l, mid);
        buildSegmentTree(rightChild(treeIndex), mid + 1, r);
        //tree[treeIndex] = tree[rightChild(treeIndex)] + tree[leftChild(treeIndex)];
        //假如我们的业务需要求分段的和，我们就可以写为+的形式
        //所以这里我们使用一个新的接口来进行两个泛型的运算
        tree[treeIndex] = merger.merge(tree[leftChild(treeIndex)], tree[rightChild(treeIndex)]);
    }

    // 返回区间[queryL, queryR]的值
    public E query(int queryL, int queryR) {
        if (queryL < 0 ||
            queryL >= data.length ||
            queryR < 0 ||
            queryR >= data.length ||
            queryL > queryR) {
            throw new IllegalArgumentException("索引不正确");
        }
        return query(0, 0, data.length - 1, queryL, queryR);
    }

    // 在以treeID为根的线段树中[l...r]的范围内，搜索区间[queryL...queryR]的值
    private E query(int treeIndex, int l, int r, int queryL, int queryR) {
        if (l == queryL && r == queryR) {
            return tree[treeIndex];
        }
        int mid = l + (r - l) / 2;
        int leftTreeIndex = leftChild(treeIndex);
        int rightTreeIndex = rightChild(treeIndex);
        //要查询的部分在右子树
        if (queryL >= mid + 1) {
            return query(rightTreeIndex, mid + 1, r, queryL, queryR);
        } else if (queryR <= mid) {
            return query(leftTreeIndex, l, mid, queryL, queryR);
        } else {
            E leftResult = query(leftTreeIndex, l, mid, queryL, mid);
            E rightResult = query(rightTreeIndex, mid + 1, r, mid + 1, queryR);
            // 最终业务决定
            return merger.merge(leftResult, rightResult);
        }
    }

    public void set(int index, E e) {
        if (index < 0 || index >= data.length) {
            throw new IllegalArgumentException("索引不正确");
        }
        data[index] = e;
        set(0, 0, data.length - 1, index, e);
    }
    private void set(int treeIndex, int l, int r, int index, E e) {
        if (l == r) {
            tree[treeIndex] = e;
            return;
        }
        int mid = l + (r - l) / 2;
        int leftTreeIndex = leftChild(treeIndex);
        int rightTreeIndex = rightChild(treeIndex);
        if (index >= mid + 1) {
            set(rightTreeIndex, mid + 1, r, index, e);
        } else {
            set(leftTreeIndex,l,mid,index,e);
        }
        // 更新每一级的范围
        tree[treeIndex] = merger.merge(tree[leftTreeIndex],tree[rightTreeIndex]);
    }

    public E get(int index) {
        if (index < 0 || index >= data.length) {
            throw new IllegalArgumentException("索引不正确");
        }
        return data[index];
    }

    // 当做满二叉树来存储，那么肯定符合完全二叉树的性质
    private int leftChild(int index) {
        return 2 * index + 1;
    }
    private int rightChild(int index) {
        return 2 * index + 2;
    }
}

堆

优先队列

  • 普通队列：先进先出FIFO

  • 优先队列：出队顺序和入队顺序无关，和优先级相关

优先队列应用很广，比如操作系统的任务调度，就需要动态选择优先级最高的任务执行；还有一个游戏的AI，当敌人来了之后会默认的攻击威胁程度最大的敌人等等，都使用了优先队列

优先队列需要实现的接口依然还是：

1
2
3
4
5
6
7
8
public interface Queue<E> {
    int getSize();
    boolean isEmpty();

    void enqueue(E e);
    E dequeue();
    E getFront();
}

但是我们可以使用不用的数据结构实现相同的功能，比如说普通的线性结构（数组，链表），比如说顺序的线性结构（保持着排序）等等，但是最好的方式是使用堆来实现，比较如下

优先队列不同实现方式性能对比

二叉堆

二叉堆是一棵完全二叉树（缺失的叶子节点都在右下方）

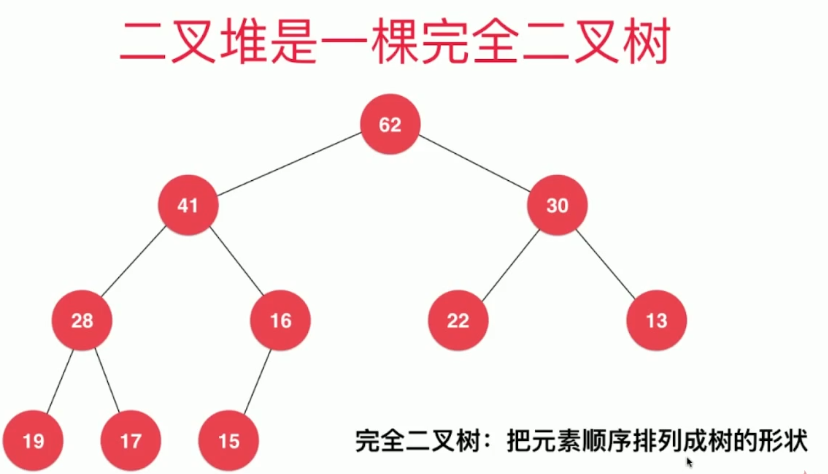
image-20200923194406290

堆的特性：

  • 一棵完全二叉树
  • 一颗平衡二叉树
  • 堆的某个节点的值总是不大于其父节点的值（最大堆）
  • 同上也有最小堆

可以使用树的结构来实现堆，但是由于堆是一棵完全二叉树，所以可以使用数组来实现完全二叉树（可以完美的对应数组的下标）

image-20200923195338585

如图，有三条性质，这三条性质就是数组下标和二叉堆结点的对应关系，而且为了防止0号空间无使用，我们略微改变了一下，就有

  • parent(i) = ( i - 1 ) / 2
  • leftChild (i) = 2*i +1
  • rightChild (i) = 2*i + 2

使用数组实现二叉堆，代码如下：（数组使用我们之前实现的数组）

  • 增添方法思想：将要添加的元素放在完全二叉树的最后一个节点，然后逐级与根节点比较，放置在一个合适的位置上

  • 删除方法思想：交换堆顶和最后一个节点，将新的头结点放置在一个合适的位置

完整代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
public class MaxHeap<E extends Comparable<E>> {
    private Array<E> data;
    public MaxHeap(int capacity) {
        data = new Array<>(capacity);
    }
    public MaxHeap() {
        data = new Array<>();
    }
    public int size() {
        return data.getSize();
    }
    public boolean isEmpty() {
        return data.isEmpty();
    }

    /**
     * 三个辅助方法：
     * 1. 返回完全二叉树的数组表示中，一个索引所表示的元素的父亲节点的索引
     * 2. 返回完全二叉树的数组表示中，一个索引所表示的元素的左孩子节点的索引
     * 3. 返回完全二叉树的数组表示中，一个索引所表示的元素的右孩子节点的索引
     */
    private int parent(int index) {
        if (index == 0) {
            throw new IllegalArgumentException("索引0：没有父亲节点");
        }
        return (index - 1) / 2;
    }
    private int leftChild(int index) {
        return 2 * index + 1;
    }
    private int rightChild(int index) {
        return 2 * index + 2;
    }

    /**
     * 向堆中添加元素
     */
    public void add(E e) {
        data.addLast(e);
        siftUp(data.getSize() - 1);
    }

    /**
     * 调整最大堆的结构
     */
    private void siftUp(int k) {
        while (k > 0 && data.get(parent(k)).compareTo(data.get(k)) < 0) {
            // 交换两个元素
            swap(k, parent(k));
            k = parent(k);
        }
    }

    private void swap(int i, int j) {
        E temp = data.get(i);
        data.set(i, data.get(j));
        data.set(j, temp);
    }

    public E findMax() {
        if (isEmpty()) {
            throw new IllegalArgumentException("堆是空的");
        }
        return data.get(0);
    }
	// 此方法也就是优先队列的出队方法
    public E extractMax() {
        E e = findMax();
        // 先将最大和最小交换位置
        swap(0, data.getSize() - 1);
        // 删除最后一个元素
        data.removeLast();
        siftDown(0);
        return e;
    }

    private void siftDown(int k) {
        // 如果左孩子都越界了，那么肯定要停止了
        while (leftChild(k) < data.getSize()) {
            int j = leftChild(k);
            // 判断有没有右孩子，且 右孩子比左孩子大
            if (j + 1 < data.getSize()
                    && data.get(j + 1).compareTo(data.get(j)) > 0) {
                j++;
                // data.get(j) 是左右孩子中的最大值
            }
            // 如果 k位置的值比他的两个孩子内更大的孩子大，说明已经完成调度
            if (data.get(k).compareTo(data.get(j)) >= 0) {
                break;
            }
            swap(k, j);
            k = j;
        }
    }
}

优先队列：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
public class PriorityQueue<E extends Comparable<E>> implements Queue<E>{
    private MaxHeap<E> maxHeap;
    @Override
    public int getSize() {
        return maxHeap.size();
    }
    @Override
    public boolean isEmpty() {
        return maxHeap.isEmpty();
    }
    @Override
    public void enqueue(E e) {
        maxHeap.add(e);
    }
    @Override
    public E dequeue() {
        return maxHeap.extractMax();
    }
    @Override
    public E getFront() {
        return maxHeap.findMax();
    }
}

类树

类树是我提的伪概念，即与普通的数很相似，但是又不是树的那些数据结构

并查集

一种由孩子节点指向父亲节点的特殊的数据结构，可以用来很方便的解决连接问题（判断是否相互连接，如网络（社交网络）中节点间的连接状态，例如一个人是否可以通过朋友的朋友认识另一个人）

并查集主要支持两个操作：

  • union(p,q)将p和q联系起来
  • isConnected(p,q)判断p与q是否有联系

并查集接口如下：

1
2
3
4
5
public interface UnionFind {
    void union(int p, int q);
    boolean isConnected(int p, int q);
    int getSize();
}

这里准备了6种实现方式，有着不同的机制或者是对方法的优化

quick find

id数组存储对应的集合，这种实现方式使得我们isConnected方法更快（O(1)级别），但是union方法会比较慢

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
public class UnionFind1 implements UnionFind {
    // 表示数据的下标，可以理解为一个指针
    private int[] id;
    
    public UnionFind1(int size) {
        this.id = new int[size];
        // 给每一个数据一个不同的下标
        for (int i = 0; i < id.length; i++) {
            id[i] = i;
        }
    }
    @Override
    public void union(int p, int q) {
        int pId = find(p);
        int qId = find(q);
        if(pId == qId) {
            return;
        } else {
            for (int i = 0; i < id.length; i++) {
                if(id[i] == pId) {
                    id[i] = qId;
                }
            }
        }
    }

    /**查看元素p和q是否在一个集合
     */
    @Override
    public boolean isConnected(int p, int q) {
        return find(p) == find(q);
    }

    /**查找元素p所对应的集合编号
     */
    private int find(int p){
        if(p<0&&p>=id.length) {
            throw new IllegalArgumentException("不正确的下标");
        }
        return id[p];
    }
    @Override
    public int getSize() {
        return id.length;
    }
}

quick union

主流的并查集的实现方式，数组中的每个元素指向，**将两个操作的时间复杂度都为O(h)**，h为树的高度

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
public class UnionFind2 implements UnionFind {
    private int[] parent;
    public UnionFind2(int size){
        parent = new int[size];
        for (int i = 0; i < parent.length; i++) {
            parent[i] = i;
        }
    }
    @Override
    public void union(int p, int q) {
        int pRoot = find(p);
        int qRoot = find(q);
        if(pRoot == qRoot){
            return;
        }
        parent[pRoot] = qRoot;
    }
    @Override
    public boolean isConnected(int p, int q){
        return find(p) == find(q);
    }
    /**找到对应的根节点*/
    private int find(int p){
        if(p < 0 && p >= parent.length) {
            throw new IllegalArgumentException("不正确的下标");
        }
        while (p != parent[p]){
            p = parent[p];
        }
        return p;
    }
    @Override
    public int getSize() {
        return parent.length;
    }
}

优化1：size

增加了一个字段sz，存储以i为根的集合中元素的个数，在Union操作的时候，我们可以将元素个数少的指向元素个数多的

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
public class UnionFind3 implements UnionFind{

    private int[] parent;
    private int[] sz;   // 以i为根的集合中元素的个数

    public UnionFind3(int size){
        parent = new int[size];
        sz = new int[size];
        for (int i = 0; i < parent.length; i++) {
            parent[i] = i;
            sz[i] = 1;
        }
    }

    @Override
    public void union(int p, int q) {
        int pRoot = find(p);
        int qRoot = find(q);
        if(pRoot == qRoot){
            return;
        }
        // -----------------这里-----------------------
        // 将元素少的合并到元素多的元素上
        if(sz[pRoot] > sz[qRoot]){
            parent[pRoot] = qRoot;
            sz[qRoot]+= sz[pRoot];
        }else {
            parent[qRoot] = pRoot;
            sz[pRoot] += sz[qRoot];
        }

    }

    @Override
    public boolean isConnected(int p, int q){
        return find(p) == find(q);
    }

    /**找到对应的根节点
     */
    private int find(int p){
        if(p<0&&p>=parent.length) {
            throw new IllegalArgumentException("不正确的下标");
        }
        while (p!=parent[p]){
            p = parent[p];
        }
        return p;
    }

    @Override
    public int getSize() {
        return parent.length;
    }
}

优化2：rank

其实我们可以直接存储树的高度，而不是元素的个数，如图

合并方式改为rank

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
public class UnionFind4 implements UnionFind {
    private int[] parent;
    private int[] rank;   // 以i为根的集合所表示的树的高度

    public UnionFind4(int size) {
        parent = new int[size];
        rank = new int[size];
        for (int i = 0; i < parent.length; i++) {
            parent[i] = i;
            rank[i] = 1;
        }
    }

    @Override
    public void union(int p, int q) {
        int pRoot = find(p);
        int qRoot = find(q);
        if (pRoot == qRoot) {
            return;
        }
        // 将树高更低的集合合并到高的集合上
        if (rank[pRoot] < rank[qRoot]) {
            parent[pRoot] = qRoot;
        } else if (rank[pRoot] > rank[qRoot]){
            parent[qRoot] = pRoot;
        }else {// 相等情况
            parent[qRoot] = pRoot;
            rank[qRoot]++;
        }

    }

    @Override
    public boolean isConnected(int p, int q) {
        return find(p) == find(q);
    }

    /** 找到对应的根节点
     */
    private int find(int p) {
        if (p < 0 && p >= parent.length) {
            throw new IllegalArgumentException("不正确的下标");
        }
        while (p != parent[p]) {
            p = parent[p];
        }
        return p;
    }

    @Override
    public int getSize() {
        return parent.length;
    }
}

优化3：路径压缩

一个并查集，我们主要实现的操作就是两个，但是在极端情况下，我们发现还是会出现树很高的现象，但其实：

路径压缩

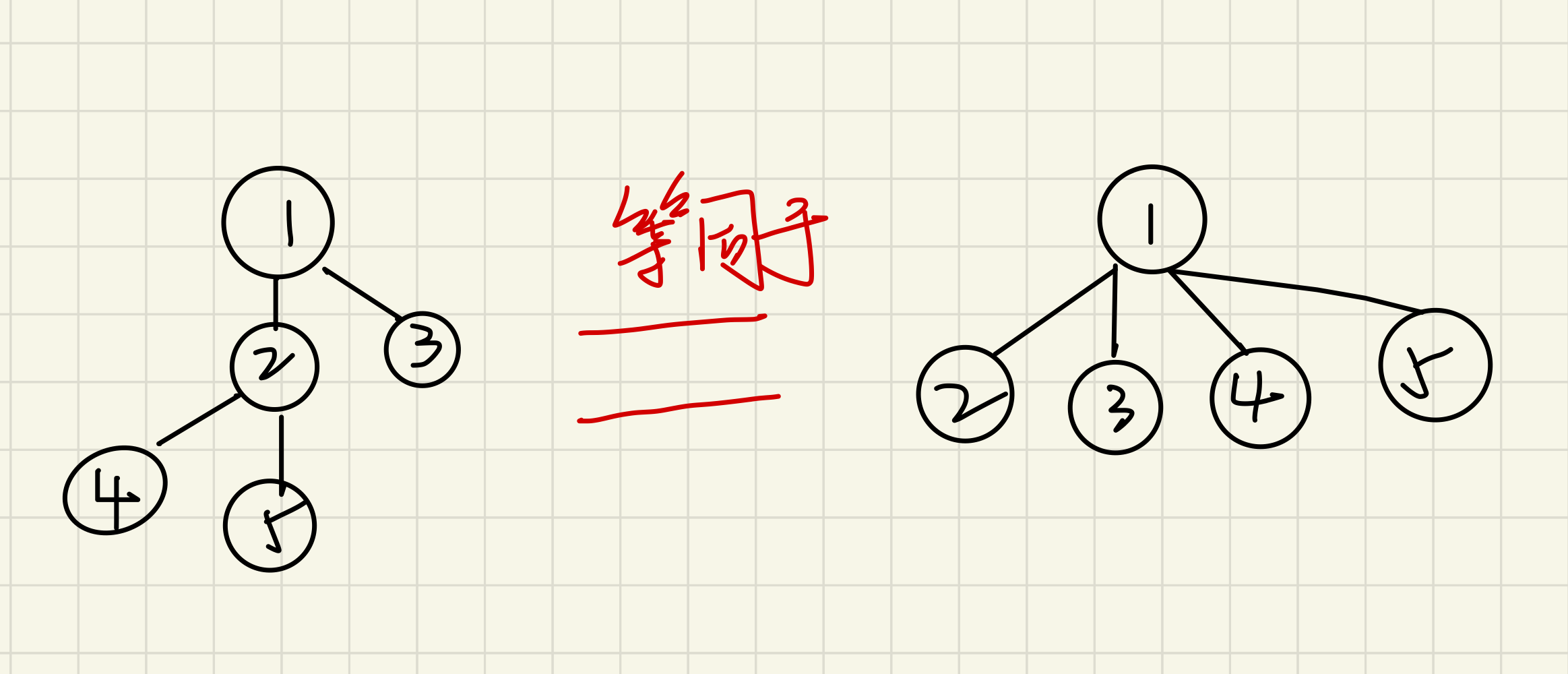
只需要优化一下find方法，我们就可以在每次find时，更改树的结构

1
2
3
4
5
6
7
8
9
10
11
12
/**找到对应的根节点*/
private int find(int p) {
    if (p < 0 && p >= parent.length) {
        throw new IllegalArgumentException("不正确的下标");
    }
    while (p != parent[p]) {
        // 就是这一行代码
        parent[p] = parent[parent[p]];
        p = parent[p];
    }
    return p;
}

这一行代码：parent[p] = parent[parent[p]];看上去很复杂，其实就是在遍历到这里时，把该节点的父节点 换成父节点的父节点

路径压缩

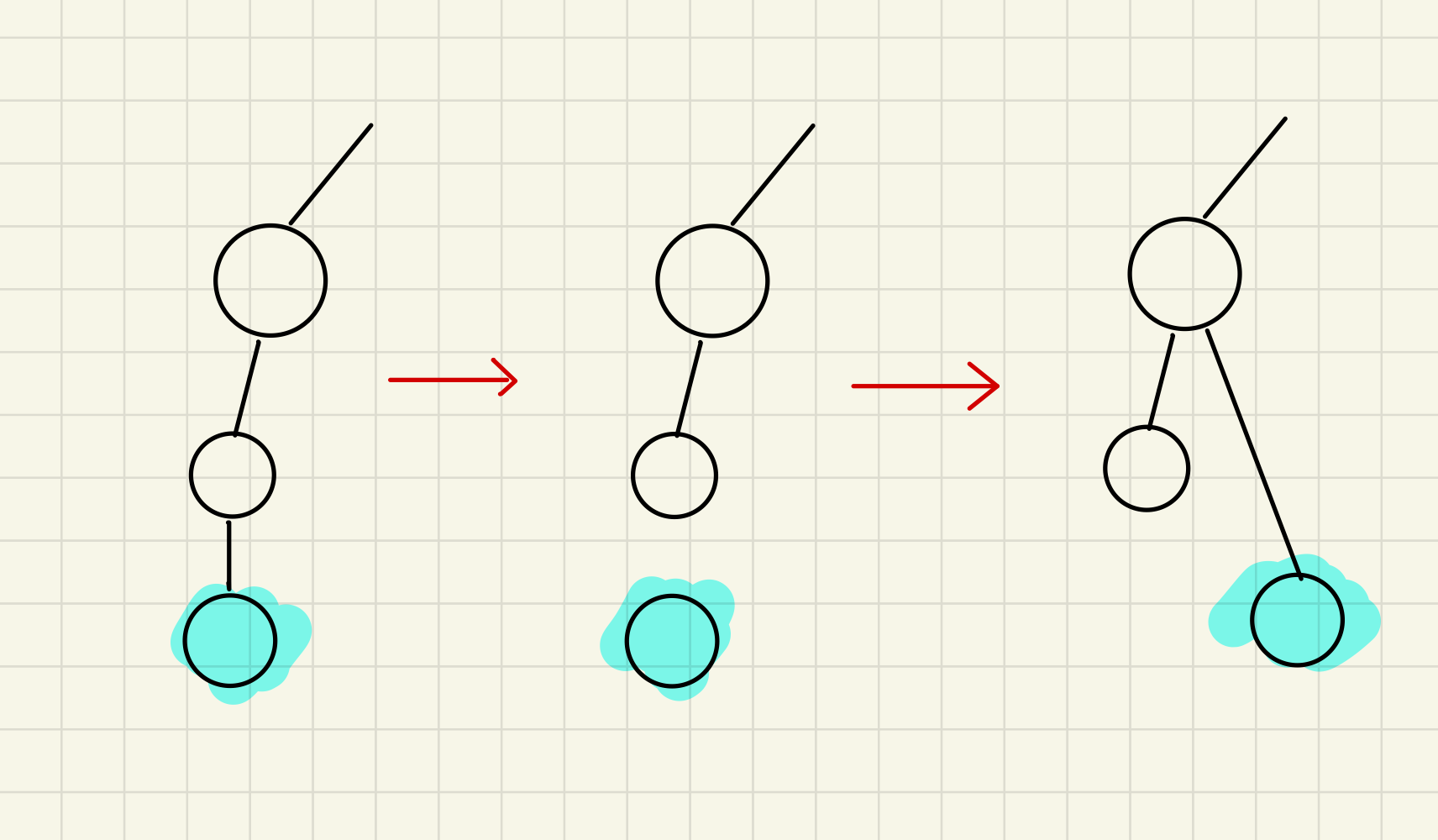
每一次find，我们都可以优化一遍，最后所有的子节点都会指向一个根，这样我们的树高大大的降低，这种路径压缩的操作，最后会

优化3：递归优化

经过路径优化后，你可能在想，为什么不直接在第一次find的时候，就将子节点连接到根节点呢？

所以我们可以这样优化

1
2
3
4
5
6
7
8
9
10
/** 找到对应的根节点*/
private int find(int p) {
    if (p < 0 && p >= parent.length) {
        throw new IllegalArgumentException("不正确的下标");
    }
    if (p != parent[p]) {
        parent[p] = find(parent[p]);
    }
    return parent[p];
}

时间复杂度分析

经过优化后，并查集的时间复杂度为O(log*n)

时间复杂度

跳表

概率算法

跳表的最底层类似一个链表，然后可以看做隔一个节点建立一个索引的结构。

跳表的数据结构可以看做：

1
2
3
4
5
6
public class Node {
    private int data = -1;
    // 存放跳转的索引
    private Node[] forwards = new Node[MAX_LEVEL];
    private int maxLevel = 0;
}

跳表是依赖于概率算法的：比如现在要新加入一个节点，需要决定该节点的层级

理论上来讲，一级索引应该占50%，二级索引占25%，三级索引占12.5%等等以此类推

决定当前节点层级是通过随机来决定的，晋升的概率为1/2。

1
2
3
4
5
6
7
8
9
private static final float PROB = 0.5 f;
private int randomLevel() {
    int level = 1;
    // 如果随机数大于0.5，就允许晋升
    while (Math.random() > PROB && level < MAX_LEVEL) {
        ++level;
    }
    return level;
}

对比红黑树

为什么跳表范围查询比红黑树快？

红黑树是老老实实一级一级查的，但是跳表是顺序和跳跃的结合，这使得跳表可以快速跳跃到目标区间的起点，而一旦找到起点后，可以直接顺序遍历底层链表。

在Redis的实现中，有序集合使用了跳表，因为对于有序Set来说，一般需要支持的操作有：

  1. 增
  2. 删
  3. 查一个数据
  4. 查区间数据

红黑树与跳表比较来说，对于前三个操作基本一致，但是查区间数据会慢一些，且实现要比跳表难一些。