Protobuf及其不同方式的测试

发表于 分类于 阅读次数： 本文字数： 12k 阅读时长 ≈ 11 分钟
引言： 2024年的第一篇：一个将压缩与编解码速度做的很好的序列化工具Protobuf

Protobuf序列化原理

protocol buffers 诞生之初是为了解决服务器端新旧协议(高低版本)兼容性问题，名字也很贴切，“协议缓冲区”。只不过后期慢慢发展成用于传输数据。

Protobuf结构

假设有json串：

1
2
3
4
5
6
7
8
{
    "userName": "Martin",
    "favoriteNumber": 1337,
    "interests": [
        "daydreaming",
        "hacking"
    ]
}

定义IDL：

1
2
3
4
5
message Person {
    required string user_name       = 1;
    optional int64  favorite_number = 2;
    repeated string interests       = 3;
}

PB会序列化为33个字节的TLV格式的bytes数组：

PB结构图

如图可见：PB的序列化原理是将原有格式序列化为TLV的字节流

  • 每一个字段都是TLV格式
    • T：不序列化字段名，tag与type打包为一个字节：tag使用5H，type使用后3L
    • L：如果是字符串就是长度；可变数字没有L标识
    • V：相应的值
  • 数字：可变长度数字
    • 比如1337，在IDL中定义为一个int64，正常来说会占用8字节，但是实际上只占用了2字节
    • 每一个字节的最高位表示是否还有后续的值，以此取代L的占用，比如 13的最高位为0, 37的最高位为1（小端存储，调转位置）
  • 数组：与Thrift不同，Pb没有type为list的形式，而是标记为重复repeated

Protobuf的数据结构(wire_type)

PB wire_type

  • 对于float、double（即32bit和64bit）：protobuf没有压缩优化
  • 对于int（即Varint）：protobuf已有优化
  • 对于String字段或是标记为Repeated的字段，都会有TLV的结构，TL就会占用2个字节

Field Tag

Field tag代替了字段名，标识字段的类型。

1
2
3
4
5
message  FeatureCtx{
  int32 intvalue = 2;
  sint32 sintvalue = 3;
}
需要注意的是：
  • 范围 1~15 中的字段编号，占用1个字节进行编码（包括字段编号和字段类型）
  • 16~2047占用2个字节
  • 19000~19999是PB自己使用的tag

比如这个string user_name = 1;，field tag占了前5位，type占用了后3位

field tag

问题1：为什么field tag占了5bit，命名可以表示最大到31，为什么只有1~15是1字节呢?

因为field tag本质也是一个Varint，因此他的最高位已经被占用了。

因此请尽量把1~15分配给常用的类型

可变数字类型

PB对Varint的优化很好，Varint 是一种紧凑的表示数字的方法。它用一个或多个字节来表示一个数字，值越小的数字使用越少的字节数。

Varint 中的每个字节（最后一个字节除外）都设置了最高有效位（msb），这一位表示还会有更多字节出现。

每个字节的低 7 位用于以 7 位组的形式存储数字的二进制补码表示，最低有效组首位。

正整数

对于int32：

  • [0, 128) 使用1个字节
  • [128, 16384) 使用2个字节
  • [16384, 2^21) 3个字节
  • [2^21, 2^28) 4个字节
  • [2^28, 2^32) 5个字节（这意味着，对于较大的数，会比int32多1字节）

Varint对于值越小的数越省空间，从统计的角度来说，一般不会消息中所有的数字都是大数。

计算逻辑是：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
char* EncodeVarint32(char* dst, uint32_t v) {
    // Operate on characters as unsigneds
    unsigned char* ptr = reinterpret_cast<unsigned char*>(dst);
    static const int B = 128;
    if (v < (1<<7)) {
        *(ptr++) = v;
    } else if (v < (1<<14)) {
        *(ptr++) = v | B; // 每个字节的最高位置为1
        *(ptr++) = v>>7; // 右移7位
    } else if (v < (1<<21)) {
        *(ptr++) = v | B;
        *(ptr++) = (v>>7) | B;
        *(ptr++) = v>>14;
    } else if (v < (1<<28)) {
        *(ptr++) = v | B;
        *(ptr++) = (v>>7) | B;
        *(ptr++) = (v>>14) | B;
        *(ptr++) = v>>21;
    } else {*(ptr++) = v | B;
            *(ptr++) = (v>>7) | B;
            *(ptr++) = (v>>14) | B;
            *(ptr++) = (v>>21) | B;
            *(ptr++) = v>>28;
           }
    return reinterpret_cast<char*>(ptr);
}

比如300：

1
2
3
4
5
6
7
300 = 256 + 32 + 8 + 4 = 1 0010 1100
v = 1 0010 1100
v | B = 1 0010 1100 | 1000 0000 =1 1010 1100 // *(ptr++) = v | B;
v >> 7 = 1 0010 1100 >> 7 = 000 0010 // *(ptr++) = v>>7;
最后结果是：
1010 1100 // Low
0000 0010 // High

负整数

对于负数，最好存储为sint类型，sint在被解析的时候采用zigzag编码

1
Zigzag(n) = (n << 1) ^ (n >> 31) // n 为 sint32 时

映射关系

将2^32分为两半，奇数表示负数，偶数表示正数。

  • 意味着sint存储的范围在[-2^31, 2^31 - 1]

问题1：pb的int32可以存储负数类型吗？占用几个字节？

int32可以存储负数类型。

如果使用int32类型存储负数，那么不管是int32还是int64位都会使用10个字节来存储（源码会强制转为）

1
2
3
4
5
6
7
8
9
10
11
12
value3 := []int32{}
value3 = append(value3, -1)
test_data3 := FeatureCtx{Int32Array: value3}

value2 := []int32{}
value2 = append(value2, -1)
test_data2 := FeatureCtx{Sint32Array: value2}

mashal_res3, _ := proto.Marshal(&test_data3)
mashal_res2, _ := proto.Marshal(&test_data2)
println(len(mashal_res3)) // 11 字节
println(len(mashal_res2)) // 2 字节

关于Packed=true的作用

PB3中默认，对基础数据类型（如整数、枚举等）的 repeated 字段都默认开启packed=true。

1
2
repeated int32 array1 = 1 [packed=true];
repeated int32 array2 = 2 [packed=false];

对于array1和arry2的区别是什么呢？

假设我们分别给他们存入4个1，即数组的内容是{1, 1, 1,1}

他们的区别是：

  • array1： T, L V, V, V, V = 2(TV) + 4(4个V) = 6bytes
  • array2： TV, TV, TV, TV = 2 * 4 = 8 bytes

“Packed”格式特别适用于 repeated 字段中包含大量相邻的小整数值的情况。

Snappy压缩原理

Snappy 使用了一个哈希表来存储已经见过的短语（通常是 4 到 11 字节的小片段）。在压缩数据时，它会扫描输入数据，并通过哈希表来查找匹配的短语。

当 Snappy 找到重复的短语时，它会用一个复制标记来表示“复制前面出现过的内容”。如果找不到匹配的短语，它就会使用字面量的方式来存储数据。

背景

目前，特征仓库的特征传递目前使用字符串逗号拼接的形式：param1,param2,param3。

预计将序列化方式进行protobuf改造，为了寻求一种更好的序列化存储方式，本文测试了使用Protobuf协议，在使用oneof、float、double等几种类型的不同序列化方式的对比。

序列化大小对比——随机数据

测试方式

四种序列化方式：

  1. 普通数组（或称为原生数组）：即idl直接定义的数组repeated float float_array = 10;

  2. oneof数组：即oneof类型的数组（oneof类型不能直接repeat）

1
2
3
4
5
6
7
8
9
10
11
12
message DataValue {
    oneof Data {
        string strVal = 1;
        int32 i32Val = 2;
        float floatVal = 3;
        double doubleVal = 4;
        int64 int64Val = 5;
    }
}
message  FeatureCtx{
	repeated DataValue data = 1;
}
  1. 占位符：并不使用数组，而是使用一个字段表示数组中的一位
1
2
3
4
5
6
7
message DataStruct {
    string sval0 = 1;
    string sval1 = 2;
    string sval2 = 3;
    string sval3 = 4;
    // 省略...
}

  1. 字符串拼接

    1. 纯小数：不同精度，使用逗号拼接：比如精度为2时，一个case是”0.11,0.23,0.12”，精度为3就是”0.222,0.333,0.122”
    2. 非纯小数：只要字符数与纯小数相同，性能就相同
      • 精度2 = 每个值的字符数是5：比如”0.12,” == “1.23,” == “12.3,”
      • 精度3 = 每个值的字符数是6：比如”0.123,” == “1.234,” == “12.34,” == “123.4,”
      • 精度4 = 每个值的字符数是7
      • 精度5 = 每个值的字符数是8
      • 精度6 = 每个值的字符数是9

数据生成方式：
int数据的生成方式：生成指定范围的数据

1
2
3
4
5
6
7
8
9
10
11
12
13
func genRandomInt(min, max int32) int32 {
    rand.Seed(time.Now().UnixNano())
    randomNumber := rand.Int31n(max-min+1) + min
    return randomNumber
}
小数的生成方式：指定生成范围以及精度
func generateRandomFloat(min, max float64, precision int) float32 {
    rand.Seed(time.Now().UnixNano())
    // 生成在指定范围内的随机浮点数
    randomValue := min + rand.Float64()*(max-min)
    // 将浮点数舍入到指定精度
    return round(randomValue, precision)
}

float数组对比

测试1：数组长度1~20（有占位符）

构造了1~20不同长度float、double数组，数组的每一个元素使用random构造，每一个小数都是纯小数（即整数部分为0）；
对于字符串类型，额外需要精度，比如精度为2即保留小数点后两位：”0.12,0.23,”

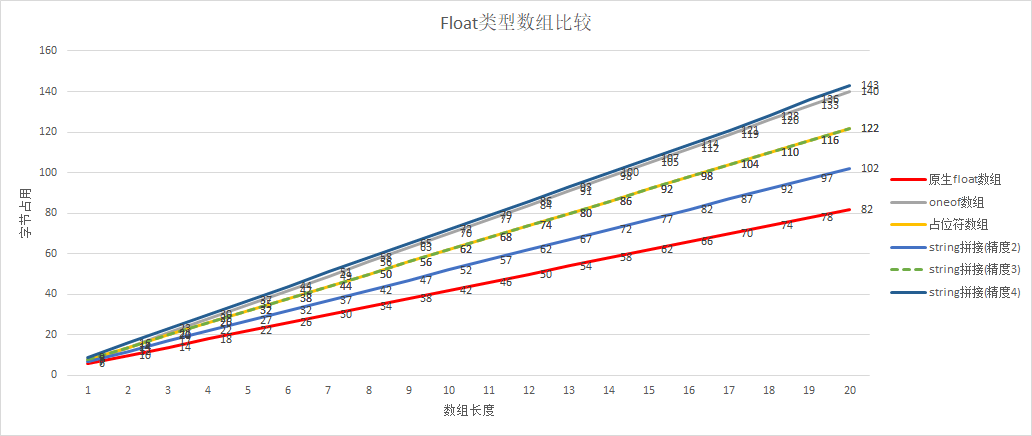Float类型比较对于float类型：
原生数组 < string拼接(精度2) < string拼接(精度3) = 占位符 < string拼接(精度4)

也能看出：占位符的性能大致为string精度为3时的性能

测试2：数组长度1~100（有snappy压缩，无占位符）

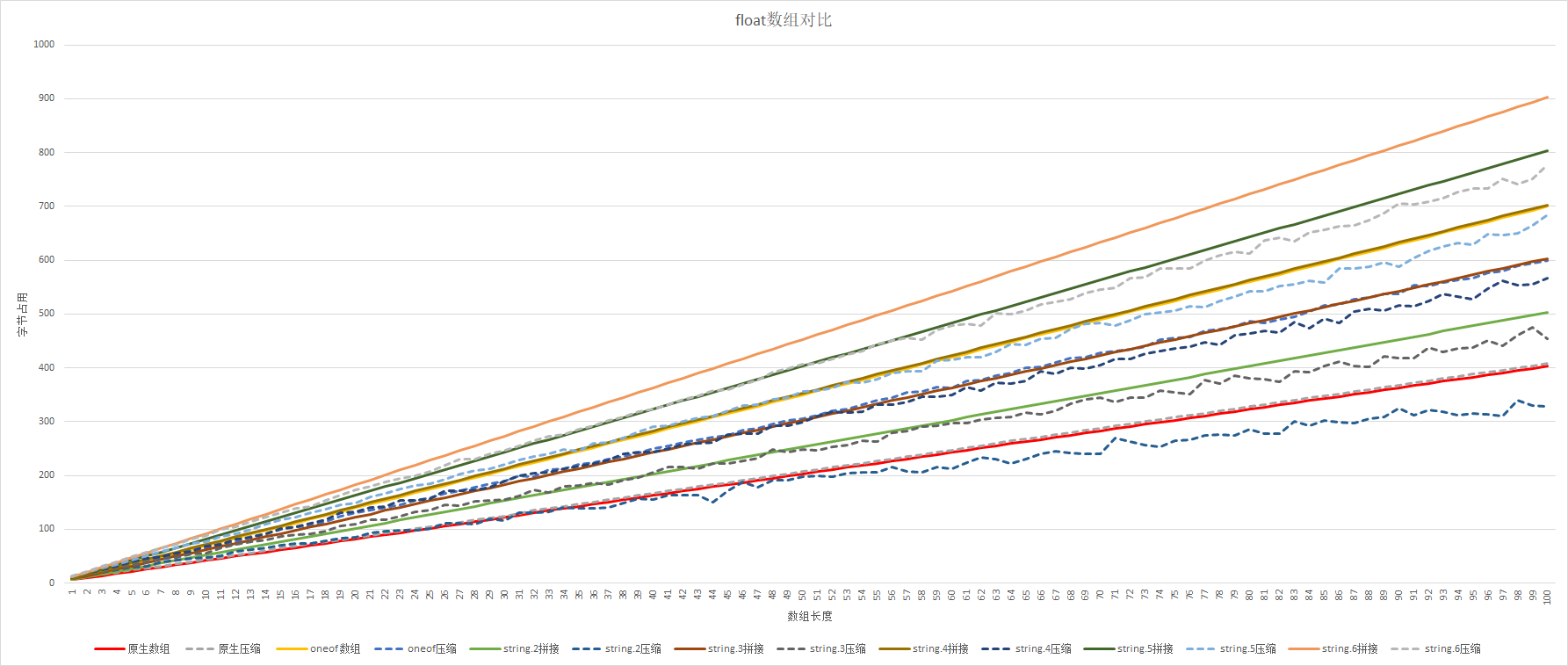
Float类型比较
1、在数据随机生成的情况下（即数据重复率很低时）有以下结论：

  • Snappy在数组长度50之后，压缩效果比较好。
  • Snappy对原生float数组压缩几乎没有效果。
  • 在数组长度大于50之后，string.2拼接略好于原生数组

2、在数据随机生成的情况下（即数据重复率很低）时，总体排序为：

string.2压缩 < 原生数组 < string.3压缩 < string.2 < string.4压缩 < string.3 = oneof 压缩 < string.5压缩 < string.4 = oneof < string.6压缩 < string.5 < string.6

3、在数据随机生成的情况下（即数据重复率很低）时，Snappy压缩率：
当数组长度为50→100

  • 原生数组压缩率：不压缩
  • oneof压缩率：87%
  • string.2压缩率：72%
  • string.3压缩率：80%
  • string.4压缩率：84%
  • string.5压缩率：86%
  • string.6压缩率：87%

4、假设string拼接方式为1，那么使用不同的序列化方式的字节占用是：（取数组长度为35时的结果）

不同精度 float数组 oneof数组 oneof数组+snappy
string.2 0.80 1.38 1.26
string.3 0.67 1.15 1.05
string.4 0.58 0.99 0.90
string.5 0.51 0.87 0.79
string.6 0.45 0.77 0.70

精度为6，使用float的优势比string拼接好一半多。

double数组对比

测试1：数组长度1~20（有占位符）

Double数组对比
对于double类型：

string拼接(精度2) < string拼接(精度3)<string拼接(精度4)<string拼接(精度5) = 原生double数组 < 占位符数组 < oneof数组

测试2：数组长度1~100（有snappy压缩，无占位符）

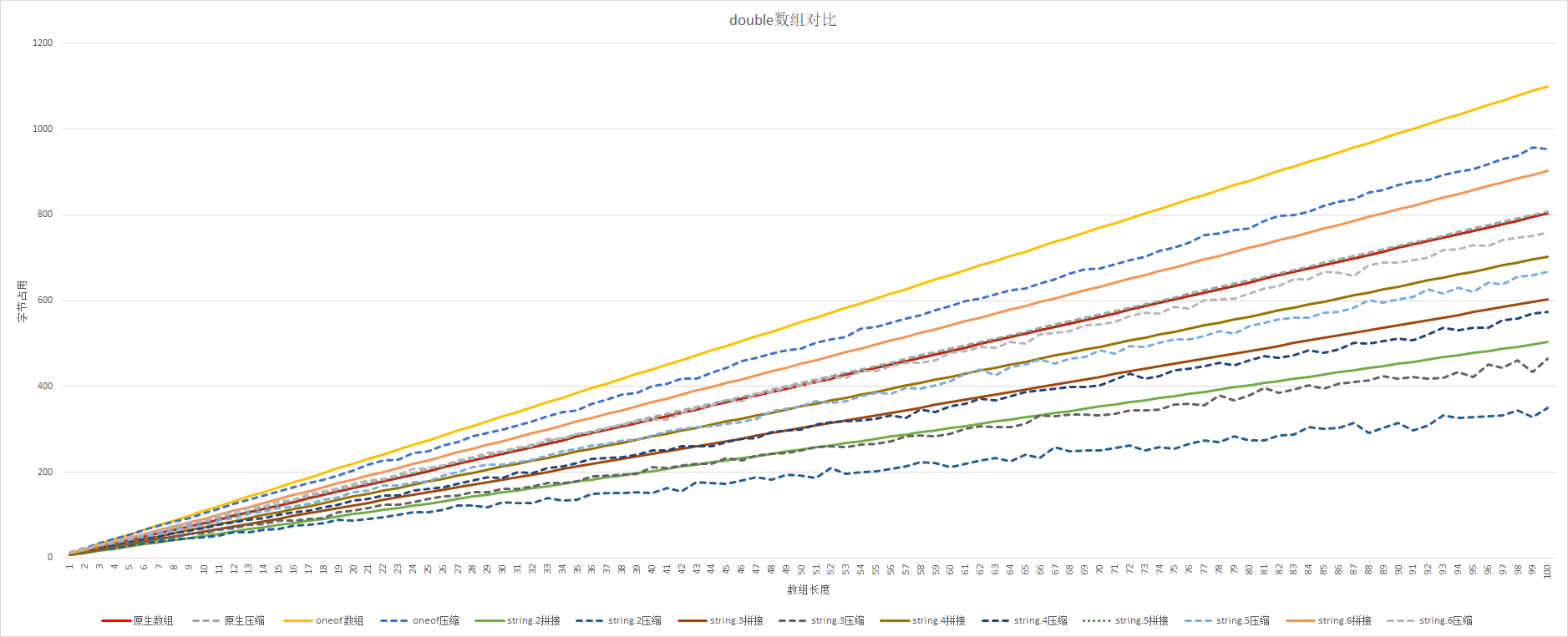
Double数组
1、整体来看：

  • Snappy对原生double数组压缩没有效果。
  • string拼接要好于原生数组（普通数组），因为pb对double没有优化，直接会直接给8字节

2、总体排序：

string.2压缩 < string.3压缩 < string.2 < string.4压缩 < string.3 < string.5压缩 < string.4 < string.6压缩 < string.5 = 原生数组 < string.6 < oneof数组压缩 < oneof数组

3、假设当前的string拼接方式为1，那么使用原生数组、压缩字符串、压缩oneof数组的占用是（取数组长度为35时的结果）

double数组 oneof数组 oneof数组+snappy
string.2 1.59 2.16 1.96
string.3 1.33 1.81 1.64
string.4 1.14 1.55 1.41
string.5 1.00 1.36 1.24
string.6 0.89 1.21 1.10

当string精度为5，double数组与string拼接基本相同。

当string精度为6，double数组好于string拼接。

int数组对比

测试1：int数组对比其他格式

由于数据的长度对String拼接的方式影响比较大，因此我们分别测试了数量级在0-100、100-1w

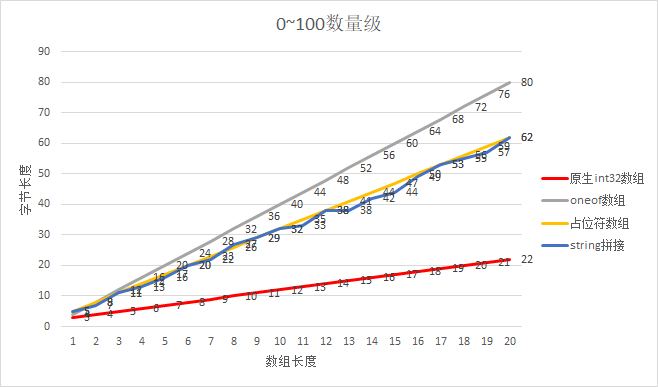
0~100数量级

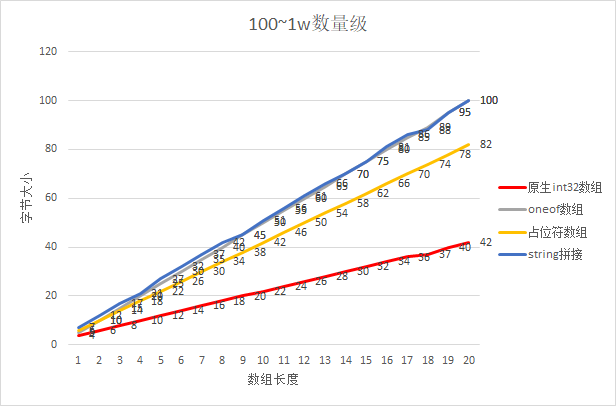
100~1w数量级

对比可见，pb对int数组的优化是十分明显的，不论数量级在什么级别，原生的int数组有压倒性的优势。

排序为：原生数组 << 占位符数组 = 0100数量级string拼接 < oneof数组 = 1001w数量级string拼接

测试2：在要求精度的前提下，对比float2int与float

要求精度accuracy的前提下，将float*accuracy存在int数组内，与直接使用float数组进行对比。

0~1数量级对比

当数据是纯小数时，约束精度是非常有效的。

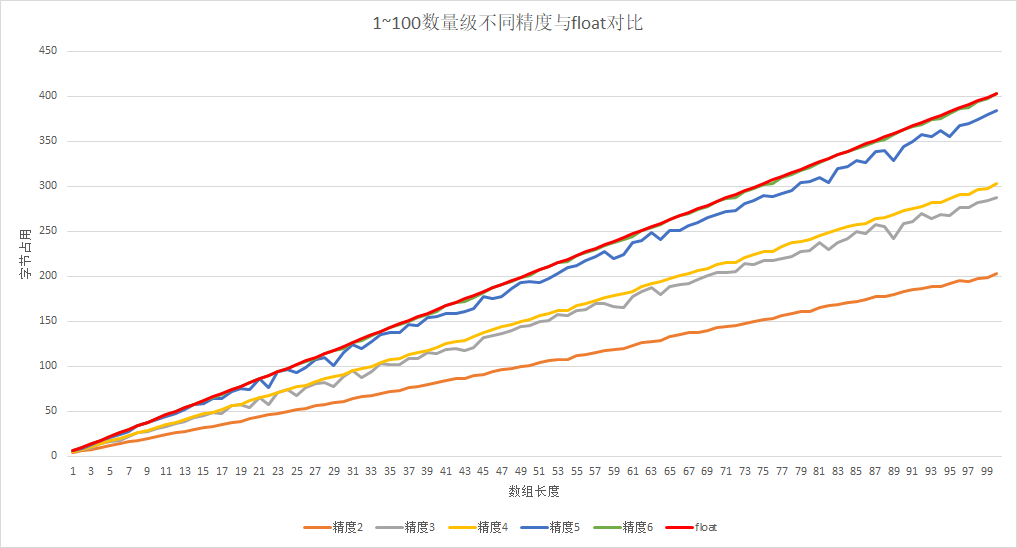
1~100数量级对比

100~1w数量级对比

随着数量级的提高，使用此方法的优势下降，此方式适合于整数部分比较少，小数部分较多的情况。
我们假设使用float为1，那么各种精度的int类型收益如表所示：

数量级 精度2 精度3 精度4 精度5 精度6
0~1(纯小数) 0.25 0.47 0.49 0.71 0.73
1~100 0.50 0.71 0.75 0.94 1.00
100~1w 0.75 0.94 1.00 1.17 2.19

PB对比总结

1、字节占用天梯图（字节占用从小到大排序）

取数组长度在30~50之间时（一个特征组的特征基本在这个区间内）

  1. int数组
  2. 占位符(int)、数据量级在0~100string拼接
  3. oneof(int)、数据量级在0~1w string拼接
  4. float数组、snappy(string.2)
  5. string.2、snappy(string.3)
  6. string.3、snappy(string.4) 、占位符(float)
  7. string.4、snappy(string.5) 、oneof数组(float)、压缩oneof(float)
  8. string.5、snappy(string.6) 、double数组
  9. string.6、snappy(string.7)
  10. string.7、oneof数组(double)、压缩oneof(double)
  11. string.N

2、使用int替代float，会在小数部分多，整数部分少的情况下有明显收益。

与现行方案string拼接对比，使用int收益如下（string不同精度 / int不同进度）

数量级 精度2 精度3 精度4 精度5 精度6
0~1(纯小数) 0.20 0.32 0.28 0.35 0.33
1~100 0.34 0.41 0.38 0.42 0.40
100~1w 0.38 0.42 0.40 0.43 0.73

序列化大小对比——真实数据

与随机生成的数据相比，真实的数据通常有几个特点：

  1. 重复率会高一点：因此Snappy压缩情况会好一点。
  2. 空值率会高一点：空值需要额外的存储。

真实的数据，可能存在为空的情况，也不好使用0这种有意义的数值表示null，因此需要存放空值的下标，关于下标的存储方式有这么两种：

  1. 可以使用int[]数组存放下标
  2. 使用int[]数组，但是每一个元素使用bitmap，每一位对标一个下标，那么总共需要length / 31个int数作为bitmap。

PS：这里使用31，而不是32，是为了避免出现负数，Protobuf的int32类型对于负数的存储不论大小，都会占用10字节。（pb对于负数的优化是sint类型）

测试数据case1

此处使用真实数据测试，但数据源不能公示，此处仅展示结论
idl：

1
2
3
4
5
6
message  FeatureCtx{
  repeated string strArray = 1;
  repeated int32 intArray = 2; // 存放值
  repeated int32 emptyArray = 3; // bitmap
  repeated float floatArray = 4;
}
  • int+int表示使用int数组存数据，且使用int数组存null值下标
  • int+bitmap表示使用int数组存数据，且使用bitmap存null值下标

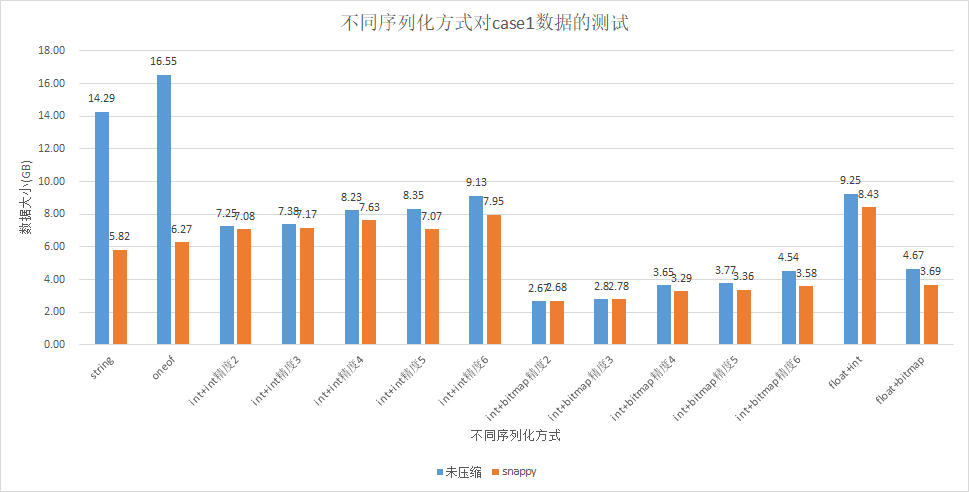
case1

表中可见：

  • 数据压缩后：int+bitmap < float + bitmap < string <oneof < int + int < float + int
  • int+int的方式表现不如string，是因为表的字段大部分为空，string拼接使用”N”来表示空，大量重复的N在压缩后效果十分明显（case1数据Null字段/全部字段=48/53）
  • snappy的压缩，对string、oneof效果最好，对基本数组的压缩很小。（之前的测试对int、float、double等类型完全没有压缩，是因为生成的数都是随机的，重复率比较小）
  • 该case数据的小数精确到4位，拿精度为4的int+bitmap对比string，比值为0.56 : 1
  • 数据null值字段 / 全部字段 = 48/53，空值很多，如果数据比较充实，那么int+bitmap的效果会比string更好。

测试数据case2

case2也是一个较为稀疏的表。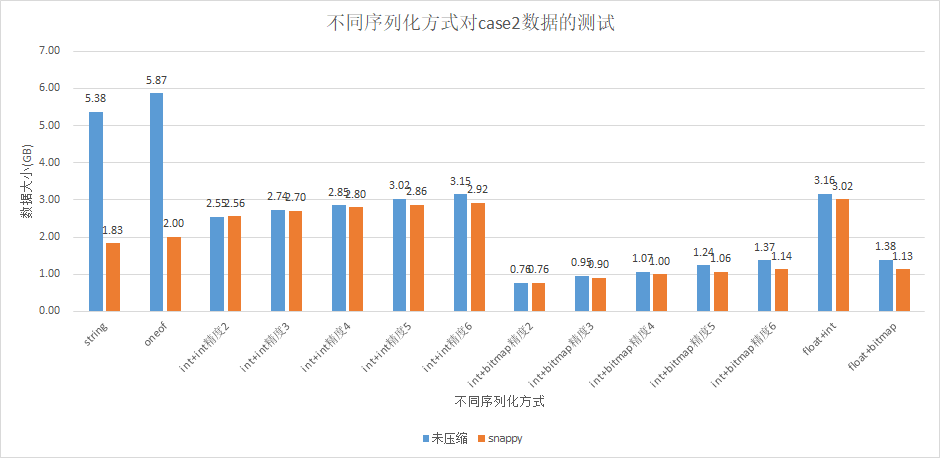
case2稀疏
我们将null的数据除去，使用剩下的字段构造一个稠密表进行测试：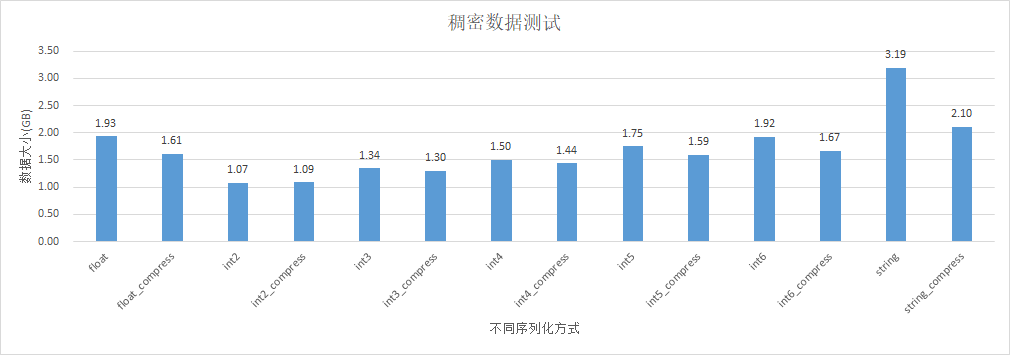
case2稠密数据
float_compress:string = 0.50以及float_compress:string_compress=0.76

测试数据case3

由于此表的数据含有int、string、bigint、float四种数据，因此不同的序列化方式的区别仅在于对于float类型，是使用int存储还是float数组存储。（对于null值的处理，除string拼接外均使用bitmap)
测试方式：
Idl：

1
2
3
4
5
6
7
8
9
10
11
12
13
message  FeatureCtx{
    repeated DataValue data = 1; // oneof
    repeated string strArray = 2; // 存放string
    repeated int32 intArray = 3; // 存放int数值
    repeated int32 emptyArray = 4; // 存放空元素下标，Array
    repeated float floatArray = 5; // 存放float值
    repeated int32 intFloatArray = 6; // 存放float值，使用 float * accuracy = int
    repeated int64 longArray = 7; // 存放float值，使用不同精度

    // tag最好在1~15，因为1~15使用1个byte
    //  optional string dataVersion = 14; //数据的版本；例如离线表Hive的分区；
    //  string metaVersion = 15;//特征组的元数据版本。
}

测试udf：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
public static Integer evaluate(String name, String version, Map<String, String> keyItems, Map<String, String> valueItems, int accuracy, int compress) throws IOException {
    // 初始化部分
    int paramSize = valueItems.size();
    // 最多使用31位，使用32会出现负数，pb的int32存储负数需要10字节
    final int bitmapSize = 31;

    List<Integer> intArray = new ArrayList<>();
    List<Integer> emptyArray = new ArrayList<>();
    int bitmapNum = paramSize / bitmapSize;
    for (int j = 0; j <= bitmapNum; j++) {
        emptyArray.add(0);
    }
    List<Long> longArray = new ArrayList<>();
    List<String> stringArray = new ArrayList<>();
    List<Integer> floatArray = new ArrayList<>();
    // 遍历参数，判断类型，放入不同的list
    int i=-1;
    for(String key : valueItems.keySet()){
        i++;
        String ele = valueItems.get(key);
        if (Strings.isEmpty(ele)) {
            int bitmap = emptyArray.get(i / bitmapSize) | (1 << (i % bitmapSize));
            emptyArray.set(i / bitmapSize, bitmap);
            continue;
        }
        String type = keyItems.get(key);
        if(type == null) continue;
        switch (type) {
            case "int":
                // 放入数组队列
                intArray.add(Integer.parseInt(ele));
                break;
            case "long":
                // 放入long队列
                // 先转为double再换为long，防止某些NaN转为0.0导致parse出错
                longArray.add((long) Double.parseDouble(ele));
                break;
            case "float":
                // 【方式1】放入float队列——int*精度
                int val = (int) (Float.parseFloat(ele) * accuracy);
                floatArray.add(val);
                // 【方式二】直接放入float队列
                // floatArray.add(Float.parseFloat(ele));
                break;
            case "string":
                // 放入string队列
                stringArray.add(ele);
                break;
        }
    }

    FeatureCtx.Builder builder = FeatureCtx.newBuilder();
    builder.addAllIntArray(intArray);
    builder.addAllEmptyArray(emptyArray);
    builder.addAllIntFloatArray(floatArray);
    builder.addAllLongArray(longArray);
    builder.addAllStrArray(stringArray);

    byte[] bytes = builder.build().toByteArray();

    if(compress == 1){
        bytes = Snappy.compress(bytes);
    }
    return bytes.length;
}

结果如下：

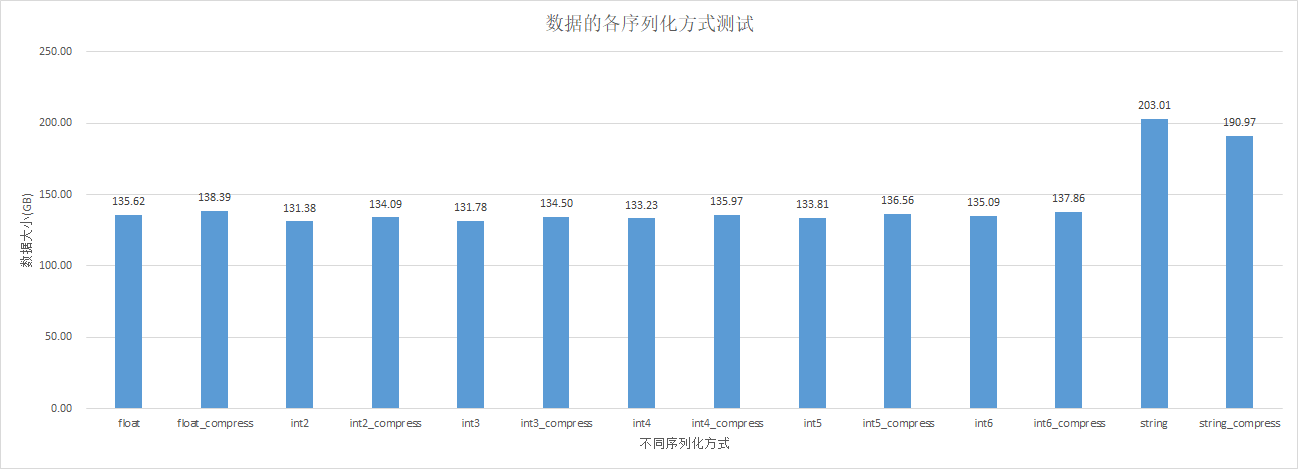
不同序列化方式测试
对比float+bitmap与string拼接比值为138 / 203 = 0.66

问题一：为什么前面六种方式的数据大小基本一致？

因为数据本身float占比很小，特征参数的统计如下：

  • Int 27个
  • String 17个
  • Bigint 1
  • Float 2

大部分都是string和int，除string外的方式，前面六种方式只对float类型有所区分而已，因此基本一致。

问题二：为什么数据压缩率不高？甚至压缩完会比原来更高

对于每一组特征，重复率不高，因此压缩率不高。
比如：使用基本的int数组或是float数组进行存储时，原本的100bytes，压缩后变为103bytes，多的3bytes存储了Snappy的数据结构，数据条数比较多（20231210分区数据：3,604,946,782条，1T数据大小），而数据本身重复率不高，空值率不高，因此压缩率不高，甚至返增。

测试数据case4

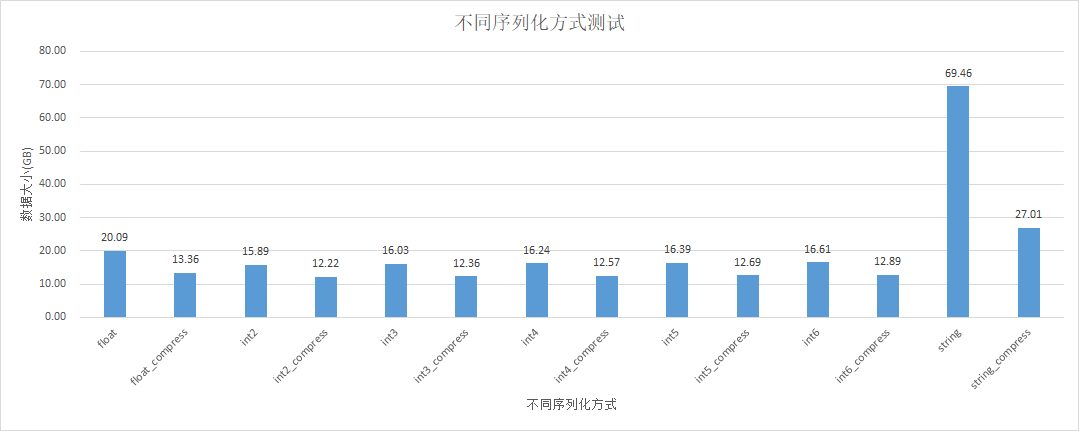
case4稀疏

float+snappy : string 比值为：20.09 : 69.46 = 0.28
float+snappy与int6+snappy压缩完大小基本一致。

测试数据case5

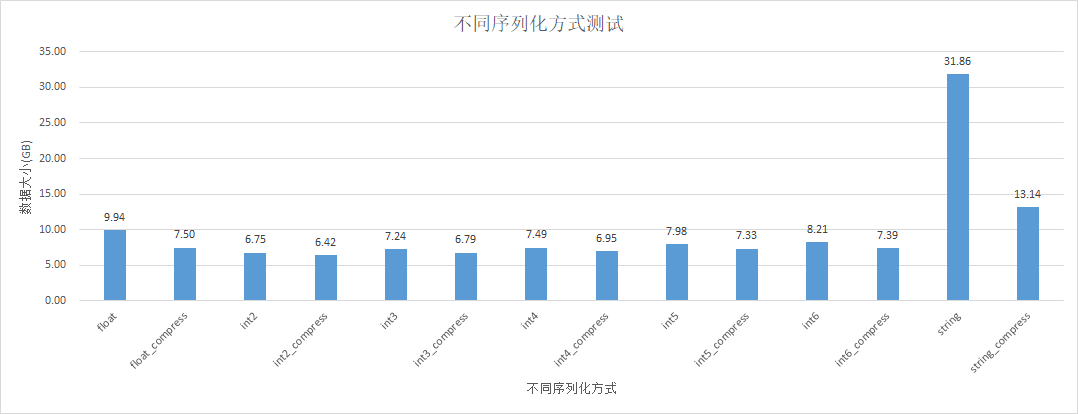
case5
float+snappy : string 比值为：7.5 : 31.86 = 0.23

float+snappy与int6+snappy压缩完大小基本一致。

测试数据case6

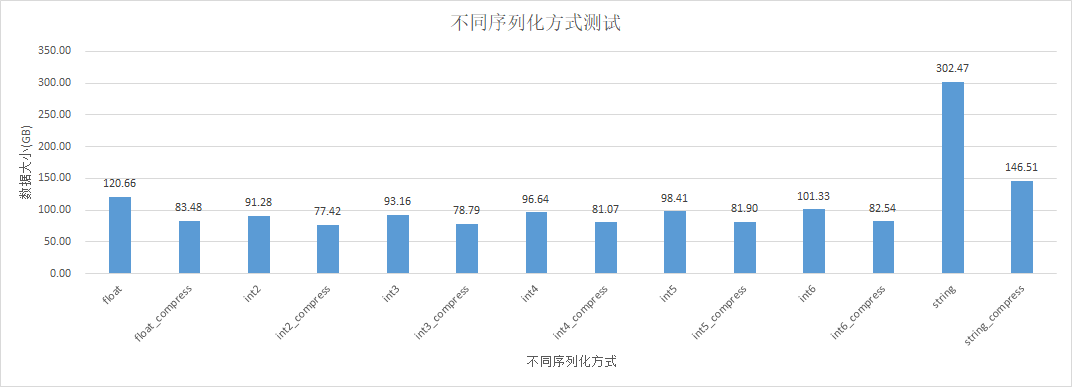
case6
float+snappy : string 比值为：83.48 : 302.47 = 0.27

float+snappy与int6+snappy压缩完大小基本一致。

PB化结论

  1. 对于不同的数据，最好使用不同的pb数据结构：

    • 对于字符串：使用字符串
    • 对于int、long：使用int32、int64
    • 对于浮点数：优先使用float数组，使用int*accuracy比float数组少一点，但是差异不大，反而引入精度问题。
    • 对于null值：使用int[]，其中每一个元素都是一个bitmap

  2. 关于snappy

    • 可以在序列化后直接加Snappy，稀疏情况下使用效果比较好（对于比较稠密的、而且重复比较少的数据，可能会增大size）

      • Snappy的原理是根据数据构造了一个重复语句的哈希表，重复越多压缩率越高。

参考文档