计算机视觉CV

发表于 更新于 分类于 阅读次数： 本文字数： 5.2k 阅读时长 ≈ 5 分钟
引言：CV 计算机视觉

CV

参考的内容：

  • CS231N 计算机视觉课程
  • 李永乐 卷积神经网络

Computer Vision

图像识别的难点：**Semantic gap **语义间隙、语义鸿沟（即我们看一张图片和计算机看一张图片之间存在一些区别）

  • 视角区别 Viewpoint Variation：稍微切换一个视角，存储的图片将会发生巨大的变化
  • 照明 Illumination： 光线昏暗明亮
  • 变形 Deformation：猫咪可能会有不同的姿势
  • 隐藏 Occlusion： 猫咪可能只露出一个小尾巴
  • 背景干扰 Background Clutter：雪地里面有一只白色猫咪
  • 类内差异Innerclass Variation：猫咪有黑、白，大、小的区别

在最一开始，科学家使用一些硬编码的方式，比如对一只猫先找边界，然后找出它的眼睛、鼻子、嘴巴，然后再去判断这是否是一只猫

但是这种方法很不优雅，不是一个通用的方法，换一个研究对象就得重新进行编码，因此提出了：数据驱动方法 Data-Driven Approach

数据驱动方法

类似于监督学习的方法

1、 首先要有一些已经加了标签的图片集

2、 使用机器学习的方式去训练一个分类器

3、 对新的图片进行预测

K近邻算法

K近邻算法通过计算两张图片像素点之间的L1或是L2范数，去求两者之间的关系

使用KNN并不是一个好的办法，它存在以下缺点：

  • 训练的时间短，但是测试的时间很长（我们通常都会希望训练的时间长点，但是测试的很快）

训练是O(1)，但是测试是O(N)

  • 2范数不太适合表示图像之间的视觉感受差异（一个图片经过平移、略微着色、去掉几个块后求出的值与原图相同，但是我们感受上却是不同的）

such as这个图：

2范数不适合表达视觉感受

  • 维度灾难：为了达到好的效果，我们需要将数据密集的分布在空间中，但是这样计算量会指数式的上升（意思是：不利于处理高维问题）

线性分类

线性分类企图去构造一条线，去判别是否是此类别的图片

使用线性分类也存在一些问题：

  • 可能存在不能使用一条线去划分的情况：比如我们人工构造这样的一种数据集是大于零的奇数、大于零的偶数，不存在一条线可以划分这两个类别
  • 范围问题：比如一个类别只在一个范围内
  • 多分类问题：比如一张图片分给多种类别

反向传播

正向传播与反向传播

反向传播是相对于前向传播而言的，如图所示，这是一个f(x) = (X+Y)*Z的例子：

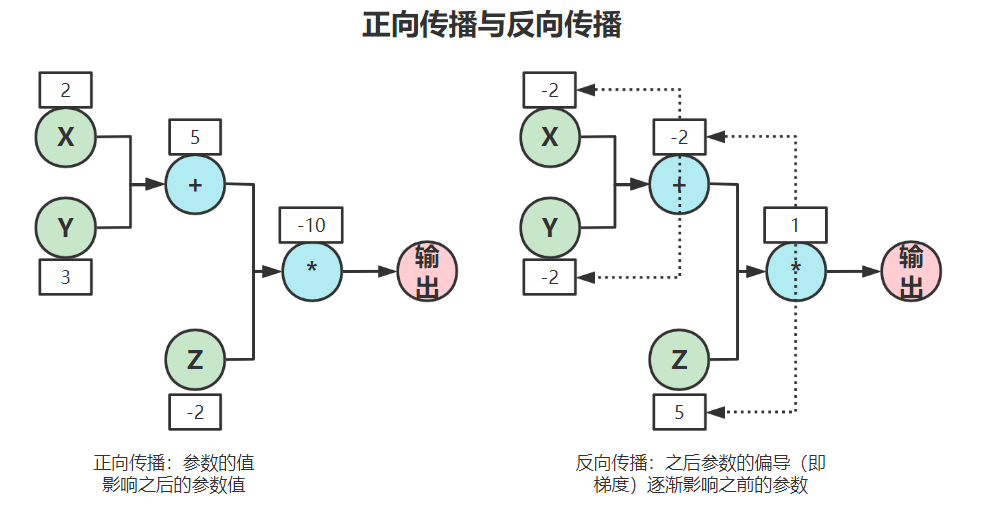
正向传播与反向传播

正向传播如图左：给XYZ分别初始值，会影响之后的结果。

反向传播如图右：从结果开始，初始化为1，分别对Z求偏导、对(X+Y)求偏导，对X和Y再分别求偏导（这也就是所谓的梯度），用来对前面的参数做一个优化，进而影响整个函数的走向

PS：为什么不直接对整个函数的积分？

这个函数是一个简单的函数，如果遇到一个比较复杂的函数，我们直接求微分是很复杂的，因此分布进行偏导，然后对每一部分求其偏导，然后不断的向前乘积，会更为简单（这样的过程称为 链式法则 Chain Rules）

不同运算的反向传播

例如这样几个运算：+ * max，我们分析一下他们的梯度其实很容易理解

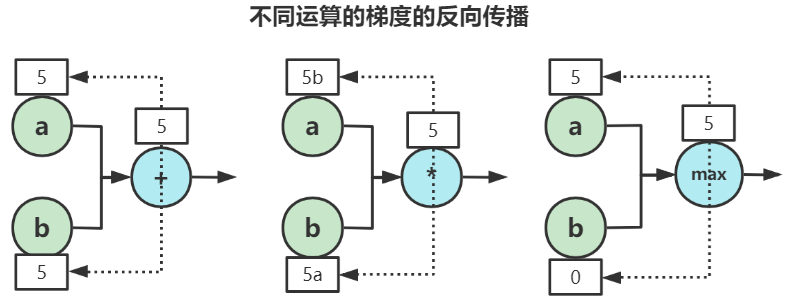
不同运算的梯度的反向传播

  • 对于加法：它的梯度会给上一级分发，比如这一级是5，传到上一级的两个分别都是5
  • 对于乘法：它的梯度会给上一级按比例转换，比如这一级是5，上一级的a=3 b=4，那么梯度传播到上一层就是a的梯度=3*b b的梯度=3*a
  • 对于max：它的梯度会分别传1与0，对于大的值回1、小的值为0，假设a>b，那么会给上一级a传1、b传0

本地梯度

对于常用的梯度传播，比如sigmoid函数，直接作为一个工具类，下一次直接复用，不需要再进行求解（常用的梯度还有很多，类库里面提供的很全）

这样的梯度称为本地梯度（local gradient）

反向传播的意义

反向传播应用在神经网络中，是一种较为容易的为了得到神经网络梯度的方法

神经网络 Neural Networks

类比于生物脑细胞的轴突、树突传递电信号，神经网络

最简单的神经网络类似于这一的函数f = A*max(0, Bx) 就是一个两层的神经网络，它的内层就是Bx、外层是一个A*x；甚至我们可以进一步嵌套，构造三层、四层甚至更深的神经网络

这里的max就是一个激活函数（Activation function），在生物中，他决定了此轴突向下传播的放电率，在神经网络内，他决定了是否将这一层的数据向下传播、传播多少

一点历史

  • 1957 Frank Rosen blatt：感知机
  • 1960 Adaline/Madaline：多层的感知机
  • 1986 Rumelhart：反向传播算法
  • 1979 福岛邦彦：神经认知，图像会沿着皮层传递信号，边缘->轮廓->细节
  • 1981 David Hunter Hubel, Torsten Nils Wiesel：观察猫对图片的反应
  • 杨立昆：提出了卷积神经网络
  • 2006 Hinton and Salakhutdinov：更高效的训练NN
  • 2010 Abdek-rahman Mohamed, George Dahl, Geoffrey Hinton：语音识别
  • 2012 Alex Krizhevsky, llya Sutskever, Geoffrey E Hinton：卷积图像分类

卷积神经网络 Convolutional NN

组合拳：卷积、池化、激活、全连接

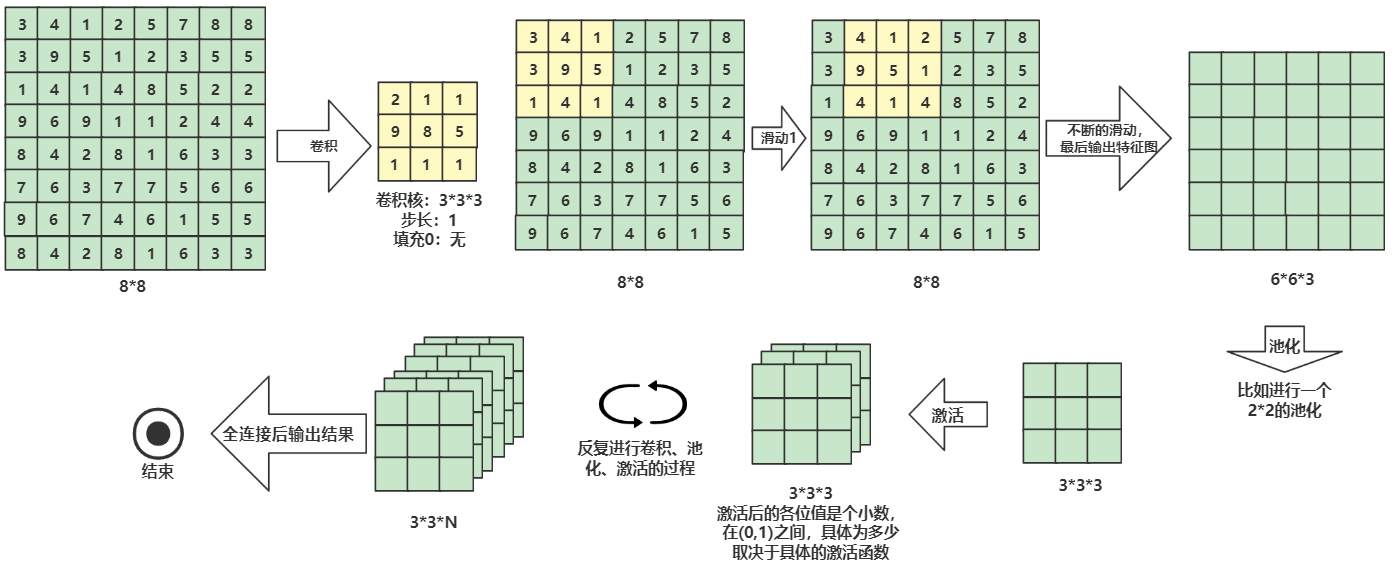
CNN组合拳

卷积：一种数学方法，使用卷积核可以提取出图像的特征

图片的存储是一张N*N的矩阵，这个矩阵的每个元素都代表了这个位置的像素点的RGB，一张图片由这么一个矩阵来组成

卷积核通常是3*3或是5*5的一个核，它会在图片上面滑动（类似于滑动窗口），每滑动一次，都会和对应的图像位置进行点积运算（对应位置相乘，然后对结果求和），新产生的这个矩阵就是该卷积核提取的关于该图片的特征矩阵

卷积核通常不止一个，常见有3个或是更多，每一个卷积核代表一个方向（可以这么理解：如果有两个卷积核，代表有x轴y轴，如果有三个卷积核，那么就代表还有一个z轴），卷积核的数量也代表了最后的结果有几个

池化：从特征矩阵中拿出最有价值的矩阵

在卷积后，池化会进一步提取有价值的数据。

比如会对特征矩阵进行一个2*2的池化，它会从各个2*2的小矩阵里，找最大的值，填充到小矩阵内

激活：决定数据是否向下传播，传播多少

池化后的小矩阵会交给下一层的激活函数，得到一个0.99,0.93,0.77...类似的矩阵，**越接近于1，说明该部分越满足卷积核的特征

卷积、池化、激活的过程可能不止一次，这是一个反复的过程

全连接：当经历过前面的完整过程后，你就是一只成功找到面包的小蚂蚁了，但是如果你想知道，是不是还有其他面包，你得去和你得兄弟们（蚂蚁大军）开个会，这个会议就是全连接，它会帮我们得到输出

知乎link

关于卷积

1、如果卷积时步长和矩阵长度不合适怎么办？

比如：一个矩阵7*7，要求步长是3，如图所示，当滑动到最后的时候，会有超出去的部分。

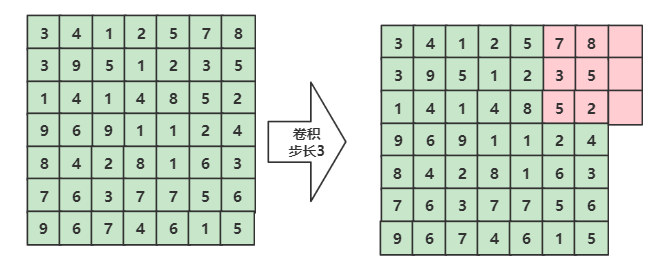
卷积步长不合适

我们可以给这个矩阵填充0，来保证我们可以进行拟合，如下图

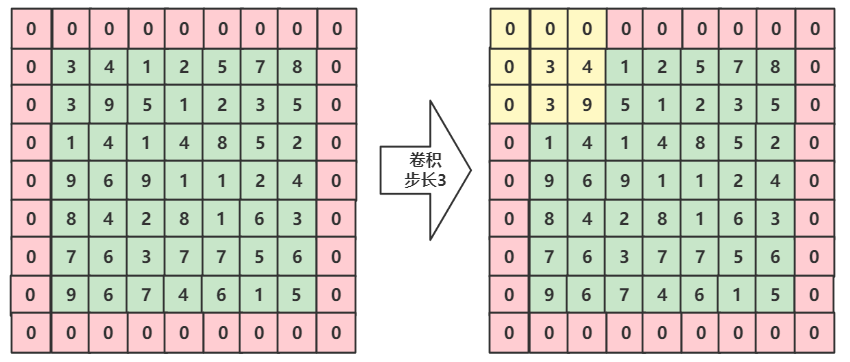
计算机网络

2、如何计算卷积后的大小？

这里有这么一个公式：

假设原有矩阵：W1*H1*D1，有K个卷积核大小为F*F，步长为S，填充为P

那么输出的结果为W2*H2*D2，其中

  • W2 = (W1 - F + 2*P)/S +1
  • H2 = (H1 - F + 2*P)/S +1
  • D2 = K

发现，如果这是一个方阵的话，那么输出也会是一个方阵

每一个卷积核有F * F * D1个参数，总共有(F*F*D1 + bias)*K（bias是偏置）

3、 eg：现在对32*32*3的矩阵进行卷积，卷积核为5*5*10，步长为1，填充为2,卷积后的矩阵大小是多少？

很容易的求出(32 - 5 + 2*2)/1 + 1 = 32，因此结果为32*32*10

关于池化

池化就是为了尽可能的使表小一点，增快训练速度，它会提取所有有价值的数据 （池化是降采样的一种方法）

最常用的方法就是最大池化 Max Pooling，当然也有均值池化等等方法

最大池化

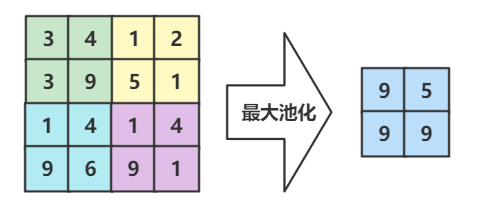
注意：一般不会在池化过程中填充0，因此一般池化的步长都会和大小相适应（池化的目的是为了降采样，而填充0就偏离了这个目的）

关于全连接

在这张图中，我们省略了关于全连接后面的步骤，这里来介绍一下

CNN组合拳

在得到3*3*N的数据后，全连接的第一步，就是将这N个矩阵拉平，拉成一个一维的序列，汇集所有的信息，得到结果

常用的参数配置

现有卷积核F*F*K，步长S，填充P

  • K通常为2的幂数：32、64、128、256等
  • 常用1：F=3 S=1 P=1
  • 常用2：F=5 S=1 P=1
  • 常用3：F=5 S=2 P=?（？代表任意）
  • 常用4：F=1 S=1 P=0

对于池化来说常用的配置为：

  • 常用1：F=2 S=2
  • 常用2：F=3 S=2

训练NN的细节

选择激活函数

激活函数的种类有很多，如图所示

激活函数

Sigmoid

Sigmoid 是一类函数的统称：

  • 有极限
  • 饱和

所以最出名的这种逻辑斯谛回归和tanh都是Sigmoid函数

逻辑斯谛回归的函数

  • 介于[0,1]之间
  • 类似于生物中神经元的放电率

关于Sigmoid有三个问题：

1、饱和的神经元会让梯度消失

所谓饱和神经元，就是当传入的X过大或者过小的时候，Sigmoid函数的两侧的导数（可以看Sigmoid图像两侧的斜率）会慢慢趋近于0

这就意味着，当数值偏高或偏低的时候，Sigmoid函数将导致无法更新梯度

2、Sigmoid不是零均值的（或者叫不是以0为中心的）

Sigmoid这一特点会导致其收敛速度较慢

关于为什么非零中心的函数会使收敛速度变慢，可以看这篇博客，非常Nice！

简单来说就是：假设输入数据全为正或是负，会导致所有的参数都向一个方向变化，假设我们有两个参数W1 W2，现在期望W1小一点，W2大一点，Sigmoid在输入数据全为正或负的情况下不可能做到让两个参数一个大一个小

3、指数运算非常耗时

tanh

  • 介于[-1, 1]
  • 以零为中心

和Sigmoid相比：tanh是以0为中心的，有利于收敛，但是仍然有在饱和情况下Kill梯度的问题

ReLU及其变种

ReLU

优点：

  • 介于[0, +无穷]，负数返回零，正数返回本身
  • 运算简单，因此卷积会很快，大约是tanh/Sigmoid的6倍
  • 正数域不会有饱和的问题
  • 也有证据表明它比sigmoid要更有生物上的合理性

也存在这么几个问题：

  • 不是以0为中心的
  • 负半轴还是会饱和（出现这种现象的时候称为 dead ReLU）

Leaky ReLU

其实就是把原本的0，换成了0.01，这个参数可以避免在负数域饱和（加了参数的ReLU称为 PReLU Parametric ReLU）

特点：

  • 不会饱和
  • 运算快（类似于ReLU）

ELU

在负数域换成了指数，避免负数域不饱和：

  • 有LU的优点
  • 基本不会饱和
  • 对噪声有更强的鲁棒性

缺点就是添加了指数，增加了运算难度

Maxout

取最大，有这几个特点：

  • 泛化了ReLU和LeakyReLU
  • 不会饱和

缺点就是将每个神经元参数数量翻倍了

激活函数小结

  • 尽量使用ReLu（小心调整学习率，防止dead ReLU）
  • 可以尝试用一下Leaky ReLU、Maxout、ELU
  • 可以试一下tanh（效果可能不会比上面的好）
  • 不要使用Sigmoid

数据预处理

拿到数据后的第一步：

  • 零均值化
  • 归一化

一般一开始只对数据做零均值化

零均值化

激活函数那里我们提到，如果数据全为正或是负，会导致收敛变慢，在一开始我们就对数据进行零均值化可以尽量避免这个问题

零均值化：将每个像素的值减去训练集上所有像素值的平均值

注意：在后续的不断的卷积过程中，还会遇到非零均值的数据，这里只能保证在第一层避免了均值化，所以还是不要使用Sigmoid

初始化权重

初始化神经网络的权值：（权值就是x前面的那个W）

【想法一】可以初始化权值为一个小的随机数，比如0.00x

使用小的随机数初始化在比较深的层次中可能会出现问题：即使一开始是标准的正态分布（高斯分布），在一层一层的卷积后，所有的激活值都会趋近于0，会让我们高斯分布小时

（在不断的W*X，最终会让结果趋近于0也很正常）

每一层激活值变化图

如图所示，一开始还是一个优雅的正态分布，到后面全变成0了

不仅如此，在反向传播的时候，由于数据非常小，也会导致我们的梯度几乎不会发生变化

【想法二】权重值给很大，比如说W=1或者W=-1

这种情况下，所有的神经元都会饱和，导致梯度不会再发生变化

【想法三】Xavier初始化：一种根据方差缩放的参数初始化

但是这种方法和ReLU效果不好（ReLU会把负数域干掉，因此方差也会干掉一半）

一个优化的办法是将输入值除以2

批量归一化

如果一个激活函数能给出近似于高斯分布，那将是极好的。通常使用批量归一化 Batch Normalization这种方法来让数据保持高斯分布

优点：

  • 这样可以提高整个网络的梯度流，允许更广范围的学习率和不同初始值下工作

超参数调优

learning rate的调优：使用cross validation，先选择部分数据、执行少量迭代；观察loss function是否下降，变化情况如何，以确定learning rate 的大致范围。

（过大则loss fucntion可能出现NaN，过小则loss function 无变化）

对超参数的采样使用随机抽样，而不是等间隔抽样，这样更容易找到更好的组合