引言：决策树既是一种分类算法、也是一种回归算法

决策树

祥见大佬的博客内容，质量很高：

• 决策树算法原理（上）
• 决策树算法原理（下）
• 决策树类库使用

信息熵

在开始决策树之前，我们需要了解几个东西：

熵：度量了事物的不确定性，越不确定其值越大。

熵的计算公式如图：

• H(x)表示随机事件x的熵

举个例子：

推广到多个变量就有联合熵：

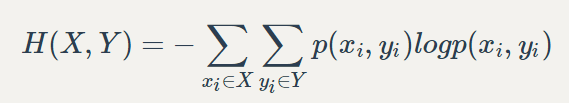
条件熵：x在知道y后的不确定性

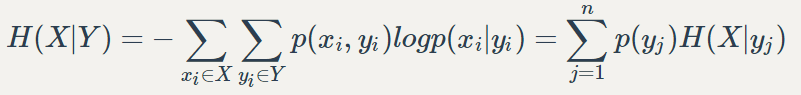
互信息或称为信息增益：x在知道y后的不确定性的减少程度

I(X, Y) = H(X) - H(X|Y)

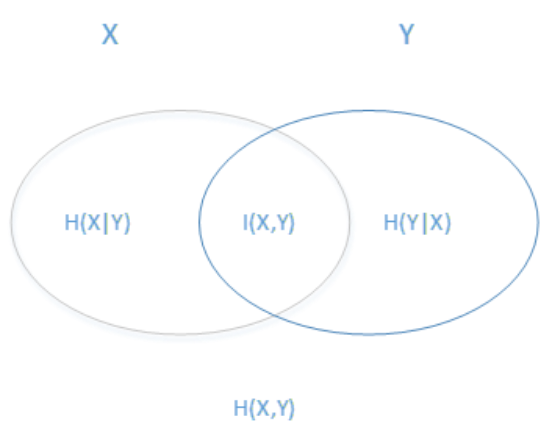
如图所示：

• 两个椭圆的并就是联合熵；
• 重合部分就是信息增益；
• 排除重合部分就是他们分别的条件熵；

决策树是什么

首先，我们有一个多个输入属性和一个输出属性的数据集：例如下面这个表格

有没有乌云	有没有打雷	会不会下雨
有	有	下雨
有	没有	下雨

然后我们需要对这个数据进行处理，从中选择一个最能区别实例的属性（比如这个例子，有没有乌云更加决定了是否下雨）

然后根据这个属性创建了树的根节点，同时创建这个节点的分支

使用这些分支，将数据集中的数据进行分类，然后重复这个过程，直至完成一棵决策树

总结一句话就是：每次选择最能区别实例的属性，重复此过程构建树

决策树的三种实现

那么如何判断一个属性是不是最能区别一个实例呢？

有三种判断方法：

1. ID3：基于信息增益
2. C4.5：基于信息增益率
3. CART：基于Gini指数

为什么C4.5不叫ID4？

那是因为决策树太火爆，他的 ID3一出来，别人二次创新，很快 就占了 ID4， ID5，所以他另辟蹊径，取名 C4.0 算法，后来的进化版为 C4.5 算法

ID3

ID3细节

1970年，昆兰提出了ID3，是最早出现的决策树的实现，它基于信息增益

根据这个表，使用C4.5算法来构建决策树：

序号	学历	婚姻	车	收入	贷款
1	专科	未婚	无	中	否
2	专科	未婚	无	高	否
3	专科	已婚	无	高	是
4	专科	已婚	有	中	是
5	专科	未婚	无	中	否
6	本科	未婚	无	中	否
7	本科	未婚	无	高	否
8	本科	已婚	有	高	是
9	本科	未婚	有	很高	是
10	本科	未婚	有	很高	是
11	硕士	未婚	有	很高	是
12	硕士	未婚	有	高	是
13	硕士	已婚	无	高	是
14	硕士	已婚	无	很高	是
15	硕士	未婚	无	中	否

1. 首先计算输出属性熵：观察输出属性“贷款”，共有是、否两种值，是占有9/15，否占有6/15

H(是否贷款)= -(9/15*log(9/15) + 6/15*log(6/15))

2. 然后分别计算每个属性的条件熵：这里以属性“学历”为例

观察到学历有三个值：专科、本科、硕士，因此各占5/15

其中：

• 专科：2/5可以贷款
• 本科：3/5可以贷款
• 硕士：4/5可以贷款

于是就如此计算H(是否贷款|学历)

H(是否贷款|学历) = 5/15*H(专科) + 5/15*H(本科) + 5/15*H(硕士)

其中分别计算每个取值的熵：

H(专科) = -(2/5*log(2/5) + 3/5*log(3/5))

H(本科) = -(3/5*log(3/5) + 2/5*log(2/5))

H(硕士) = -(4/5*log(4/5) + 1/5*log(1/5))

4. 计算信息增益I(是否贷款，学历)

I(是否贷款，学历) = H(是否贷款) - H(是否贷款|学历)

5. 计算其他属性的信息增益
6. 比较不同的信息增益，建立树

ID3存在的问题

ID3算法的过程就是这样，简单方便，这里我们值得去思考这几个问题：

• ID3没有考虑连续特征，比如长度、密度
• 在相同条件下，取值比较多的特征比取值少的特征信息增益大
• 缺少对缺失值情况的
• 没有考虑过拟合的问题

C4.5

C4.5的优化

昆兰改进了ID3算法：

ID3没有考虑连续特征

C4.5中将连续变量离散化

假设有属性为长度有四个值10、11、12、13，C4.5把连续变量求其两两相邻的平均数得到三个值10.5、11.5、12.5，然后计算三个值对于的信息增益

最后选择最大的信息增益值作为分离点，大于此值的为1，小于的为0

在相同条件下，取值比较多的特征比取值少的特征信息增益大

C4.5改用信息增益率代替信息增益

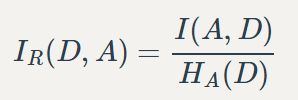
其中分母为

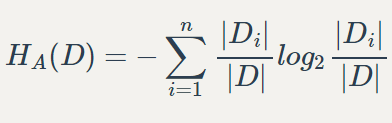
缺少对缺失值的处理

第三个缺失值处理的问题，主要需要解决的是两个问题：一是在样本某些特征缺失的情况下选择划分的属性；二是选定了划分属性，对于在该属性上缺失特征的样本的处理

翻译一下就是：

• 选择特征属性时：在有缺失情况下，如何选择最优属性进行子树划分。
• 缺失样本的处理：选择好属性后，属性缺失样本划入哪个子节点。

可以看这两篇blog：

• 缺失值处理
• 实例

没有考虑过拟合的问题

C4.5引入了正则化和剪枝。

我们还是用上一节的那个例题：

1. 在计算出信息增益I(是否贷款，学历)后
2. 分母为H(学历) = -(5/15*log(5/15)+ 5/15*log(5/15) + 5/15*log(5/15))
3. 使用1与2做除法，就得到了信息增益率，之后的步骤与ID3一样

C4.5存在的问题

• 生成的是多叉树，对于计算机来说二叉树效率会更高
• 只能用于分类
• 有大量的耗时的对数运算, 如果是连续值还有大量的排序运算

CART

CART细节

CART 分类树算法使用基尼系数来代替信息增益比，基尼系数代表了模型的不纯度，基尼系数越小，则不纯度越低，特征越好。这和信息增益 (比) 是相反的。

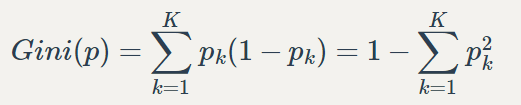
• pk代表第k个概率

当这是一个二类分类的时候（即p0 + p1 = 1）：

基于基尼系数有这么几点弥补了C4.5的缺点：

• 基尼系数会生成二叉树而不是多叉树
• 基尼系数运算比求对数运算简单很多
• 可以分类，也可以回归

对于连续值，CART与C4.5处理的步骤一样

但是有一个区别：如果当前节点为连续属性，则该属性后面还可以参与子节点的产生选择过程

CART 分类树使用的方法不同，他采用的是不停的二分

假如一个特征A有A1、A2、A3三个特征值。如果是C4.5的话，那么就会出现三个岔；如果是基尼系数的话，他会分为{A1}与{A2、A3}、{A2}与{A1、A3}、{A3}与{A1、A2}三种情况，这样还是一颗二叉树

CART的回归树与分类树

回归树和分类树的区别：

区别在于样本输出，如果样本输出是离散值，那么这是一颗分类树。如果果样本输出是连续值，那么那么这是一颗回归树

在CART中，分类树与回归树唯一的区别就是在对于连续值的处理有些不同（这部分可以去看刘建平大佬的博客）

对于连续值，回归树使用均方差，而回归树使用基尼系数。

CART剪枝策略

这是为了解决决策树一直都存在的一个问题——容易过拟合

CART使用后剪枝法

后剪枝法：先生成决策树，然后产生所有可能的剪枝后的CART树，然后使用交叉验证剪枝效果，选择最好的剪枝策略

可以分为两步：

1. 从原始决策树生成剪枝后的CART树
2. 交叉验证效果，选择最好的剪枝后的CART树

（关于CART剪枝详见大佬的博客）

CART存在的问题

• 有些时候，最优选择不是由一个特征决定的（三种算法都存在这个问题）
• 如果样本发生一点点改动就会影响整个树的结构

对比ID3、C4.5、CART

算法	支持模型	树结构	特征选择	连续值处理	缺失值处理	剪枝
ID3	分类	多叉树	信息增益	不支持	不支持	不支持
C4.5	分类	多叉树	信息增益率	支持	支持	支持
CART	分类、回归	二叉树	基尼系数、均方差	支持	支持	支持