机器学习概述
机器学习概述
赫尔伯特·西蒙:如果一个系统能够通过执行某个过程改进它的性能,这就是学习
机器学习的步骤
大致分为六个步骤,其中某些专有名词我们之后专门解释:
- 得到一个有限的训练数据集合
- 确定假设空间
- 确定学习策略
- 实现求解最优模型的算法
- 选择最优模型
- 对新数据进行预测或分析
机器学习分类
分为监督学习、无监督学习、强化学习三种,有时包括半监督学习、主动学习
本文只介绍监督学习
监督学习
监督学习的基本过程
串一下专有名词(专有名词具体解释在基础概念内解释),以便于清晰的理解监督学习的过程
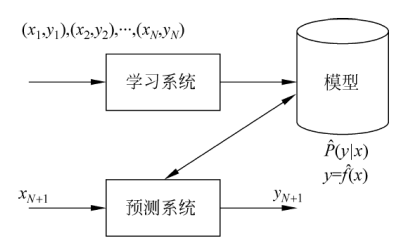
首先,我们需要一个数据集,这个数据集应该被分为三类:训练集、验证集、测试集
其次我们需要确定我们的假设空间,这是一个概率问题?还是一个非概率问题?
假设空间确定后,我们需要选择其中一个合适的模型,如何进行选择是一个很重要的问题,这也是我们需要决定的策略
一般有经验风险最小化和结构风险最小化两种策略,他们通过不同的方式尽量使经验风险趋近于期望风险
选择经验风险最小化是很简单,但是很容易出现过拟合现象,因此给经验风险加上了正则化项
这样在选择了具体的模型后,我们就可以使用训练数据训练模型了,同样为了防止过拟合,我们可以进行交叉检验,选择验证数据误差最小的一个作为最优解
基础概念
监督学习的专有名词有很多,这里做一个罗列,在阅读文章时遇到新名词可以来这里Search一下
输入空间、输出空间
其实就是输入与输出的集合
特征空间
关于这部分可以参考:线性代数——特征值与特征向量
2
# λ表示特征值,x表示特征向量,A是给定的矩阵当只有尺度变化,而没有方向变化时(或者说这个矩阵只有伸缩,没有旋转),这类特殊的向量就是矩阵的特征向量 eigenvector,特征向量的尺度变化系数就是特征值 eigenvalue。
对于具体数据来说,特征就是属性(比如一个人的数据,它的特征就是它的年龄,特征向量就是(年龄,性别等)特征组成的向量)
对于一个数据集合,每一个具体的输入都是一个实例 Instance或称为特征向量 feature vector
实例完全可以理解为就是特征向量
特征空间(eigenspace)是具有相同特征值的特征向量与一个同维数的零向量的集合
联合概率分布
联合概率就是
P(AB):即AB事件同时发生的概率
机器学习的前提就是随机变量X与Y服从联合概率分布(这句话的意思就是我们假设输入与输出存在一定的统计规律,否则我们的研究将没有任何意义)
模型与假设空间
假设空间 hypothesis space:即模型的集合
模型:输入空间到输出空间的映射(机器学习中,模型可以是概率模型或是非概率模型,分别用
P(y|x)与y=f(x)表示)
可能不是很好理解,这里举一个例子:
假设我们已知一个问题是线性关系,那么此时的模型就是一个线性函数,假设空间就是所有的线性函数
样本与样本点
样本就是样本点
样本:输入与输出对(注意,一个成对的输入和输出才是一个样本)
比如这样的一个训练数据集合:T={(x1,y1),(x2,y2)...(xn,yn)}
(x1,y1)就是一个样本,x是输入,y是输出
决策函数与条件概率分布
机器学习的模型有这两种:决策函数y=f(x),条件概率分布为P(y|x)
欧式空间
R表示实数域
R^n表示一个n维的向量空间,每一个向量都由R中的实数组成
欧式空间,别名也叫参数空间
损失函数(代价函数)
损失函数 loss function或称为代价函数 cost function:是一个用f(X)和Y表示的非负值函数,用L(Y, f(X))表示
常见的损失函数有四种:
- 0-1损失函数
1 | L(Y, f(X)) = 1, Y!=f(X) |
- 平方损失函数:
L(Y, f(X)) = (Y-f(X))^2 - 绝对损失函数:
L(Y, f(X)) = |Y-f(X)| - 对数损失函数(对数似然损失函数)
L(Y, P(Y|X)) = -logP(Y|X)
损失函数值越小,模型越好
风险函数(期望损失)
风险函数就是期望损失,用Rexp表示
期望损失:损失函数的期望
期望损失是无法具体得到的,我们只能通过经验损失来模拟期望损失
期望损失最小的模型就是我们要选择的模型
经验损失
经验损失:模型
f(X)关于训练集的平均损失,用Remp表示
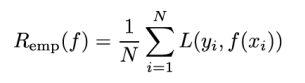
根据大数定律,当N趋近于无穷时,经验损失趋近于期望损失
策略
如何选择最优模型?
通过经验损失吗?但是由于我们的训练数据有限,因此经验风险并不理想(也就是N不趋近于无穷,经验损失也就不趋近于期望损失)
因此监督学习有两个基本策略:
- 经验风险最小化 ERM
- 结构风险最小化 SRM
经验风险最小化
经验风险最小化ERM策略认为:经验风险最小的模型就是最优模型
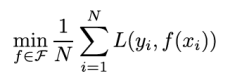
- 那个类似于F的字符表示假设空间
- 比如极大似然估计就是经验风险最小的一个例子,这也是频率派的主张
缺点:
由于我们的训练数据有限,因此经验风险并不理想(也就是N不趋近于无穷,经验损失也就不趋近于期望损失)
由于样本容量小,因此这种判断方式很有可能出现过拟合现象
结构风险最小化
结构风险最小化策略认为,结构风险最小的模型为最优模型
什么是结构风险?
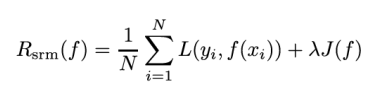
- 在经验损失的基础上加了一项模型的复杂度
J(f)表示模型的复杂度,模型越复杂越大,反之越小λ系数用来权衡经验风险和模型复杂度- 最大后验概率估计就是一个结构风险最小化的一个体现,是贝叶斯学派的主张
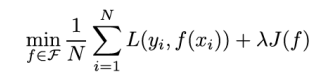
算法
学习模型具体的计算方法
过拟合现象
过拟合 over-fitting:模型出现对训练数据(已知数据)预测的很好,但是对测试数据(未知数据)预测的很差的现象
训练误差与测试误差
训练误差 training error:模型关于训练数据的经验损失
测试误差 test error:模型关于测试数据的经验损失
泛化能力
即模型预测新数据的能力
正则化
正则化等价于结构风险最小化
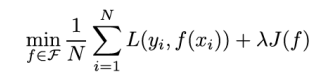
λJ(f)也称为正则化项 regularizer或罚项 penalty term,模型越复杂越大- 正则化项可以取不同的形式,比如L1范数、L2范数
- 正则化符合奥卡姆剃刀原则
- 正则化项对应与模型的先验概率
奥卡姆剃刀原则:能够很好解释数据并简单的才是最好的模型
交叉验证
为了防止过拟合现象,我们也可以把样本数据分为三类:训练数据、验证数据、测试数据
验证数据是为了用于模型选择,我们应该选择验证数据最小误差的模型
验证的方法通常使用交叉验证cross validation:
- 简单交叉验证:即随机将数据分为两部分,一部分为训练集、一部分为验证集
- S折交叉验证:均分为S份,每次利用S-1个训练,用余下的一份进行验证(比如我们分为10份,第一次我们使用2-10号训练,1验证,第二次使用1,3-10训练,2验证,以此类推)
- 留一交叉验证:S=数据集容量的特殊情况
泛化误差上界
泛化误差就是期望风险
泛化误差上界用来比较两个模型的优劣(类似于比较两个算法的时间复杂度以确定哪个好)
生成模型与判别模型
监督学习方法可以分为生成方法和判别方法,对应的模型就是生成模型与判别模型
- 生成方法:根据输入数据和输出数据之间的联合概率分布确定条件概率分布
P(Y∣X) - 判别方法:则直接学习条件概率分布
P(Y∣X)或决策函数f(X)
简而言之:生成方法需要研究数据集的分布,而判别方法直接使用条件概率公式或是决策函数
生成方法具有更快的收敛速度和更广的应用范围,判别方法则具有更高的准确率和更简单的使用方式。