概率论概念深入理解

发表于 更新于 分类于 阅读次数： 本文字数： 3.5k 阅读时长 ≈ 3 分钟
引言：概率论是另一种用数学看待真实世界的工具

概率论概念深入理解

在历史长河中，对概率的认知是有一个过程的，对概率的认知不同，分为了两个派系：频率学派与贝叶斯学派

频率学派

古典概率模型

频率学派的依赖的基础是古典概率模型，这种模型的特点是：

  • 包含有限个基本事件
  • 每个基本事件发生的概率相同

比如投骰子、比如投硬币，这些都是古典概率模型的体现

投硬币一次是否能出现正面，我们并不确定，但是随着不断的投掷，我们会发现，正反面出现的次数几乎相同，这就是频率学派眼中的概率——其实是一个可独立重复实验出现单个结果频率的极限

古典概率中，事件A的概率计算公式为：

古典概型概率计算公式

  • n表示所有基本事件的数量
  • k表示发生A事件的基本事件数目

比如，投一个骰子，点数小于3的概率为P(A) = 2 / 6

条件概率

古典概率针对的是单个事件，这种事件之间相互独立，互不影响，为了处理这种互相影响的情况，引入了条件概率conditional probability

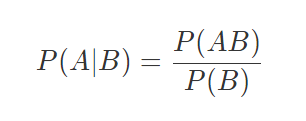
条件概率公式

  • P(A|B)表示在B事件发生的条件下，A事件发生的概率
  • P(AB)表示A和B共同发生的概率，也叫联合概率 joint probability
  • 如果联合概率P(AB) = P(A) * P(B)，那么说明A与B相互独立
  • 对于相互独立的事件P(A|B) = P(A)

基于条件概率，可以得出全概率公式 law of total probability：

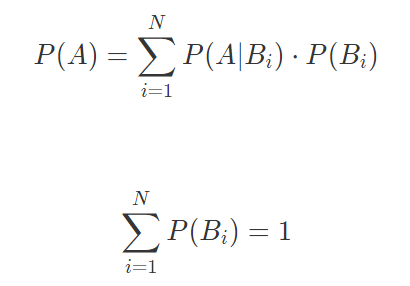
全概率公式

全概率公式的意义在于：将复杂事件的概率求解 转化为 在不同情况下发生的简单事件的概率求和

这也是频率学派的核心观点，即：先做出假设，再在这些假设的前提下讨论随机事件的概率

贝叶斯学派

而贝叶斯学派则是：在事件结果已经确定下，推断假设发生的可能性

（或者说，事后诸葛亮，结果发生后推断其可能的原因，我们需要事先拟定一些假设）

贝叶斯定理

对全概率公式稍作整理就可以得出逆概率理论，因为首先由英国牧师托马斯·贝叶斯提出，所以叫贝叶斯公式：

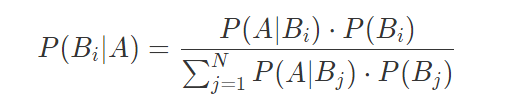
贝叶斯公式

推到过程很简单，只需要套入全概率公式和条件概率公式就可以得到，建议手推一下

进一步抽象，就可以得到贝叶斯定理 Bayes’ theorem（两步条件概率公式推导即可）

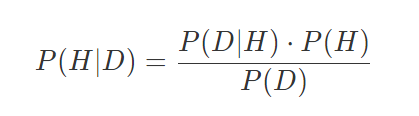
贝叶斯定理

  • H表示我们的假设，D表示数据
  • P(H)表示先验概率（prior probability）：即假设成立的概率
  • P(D|H)表示似然概率（likelihood function）：在假设H成立的条件下，可以观测到结果D的概率
  • P(H|D)表示后验概率（posterior probability）：在观测到结果的前提下，假设成立的概率

贝叶斯派关注的核心是后验概率，而且贝叶斯学派认为概率描述的是随机事件的可信程度

比如预测今天85%的概率下雨，这就不能理解为频率了，而是得理解为明天下雨的可信度是85%

贝叶斯定理应用的经典问题：

有一种病在人群中的患病率是1%，其检查结果的可靠程度是95%，也就是得病的人95%会得到阳性结果，没得病的人95%会得到阴性结果。如果一个人检查的结果是阳性，那他得病的概率是多少？

解：

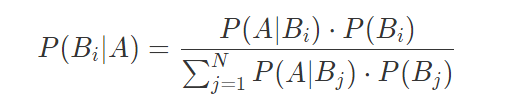
贝叶斯公式

套用到公式，此题的B1事件就是有病，B2事件就是没病，N就为2；A事件是结果为阳性的概率

1
2
3
4
5
6
7
8
9
P(B1|A) =  P(A|B1) * P(B1) /( P(A|B1)*P(B1) + P(A|B2)*P(B2) )

由题意知：
得病的概率 P(B1) = 0.01
没病的概率 P(B2) = 0.99
本身有病检测为阳性的概率 P(A|B1) = 0.95
本身无病检测为阳性的概率 P(A|B2) = 1-0.95 = 0.05
全部代入得：
P(B1 | A) = 16.1%

结果大吃一惊，检测为阳性有病的概率竟然这么低

学院派和贝叶斯派的区别

参考知乎，他们最大的区别在于认为参数空间不同

频率学派认为：数据都是在某个参数条件下产生的，一个模型中的参数是“固定”的，而数据是在分布中随机采样的。

（即：我们相信这个分布的参数不管你怎么采样，根据参数对其的估计都应该是不会变的。如果根据数据估计出来的参数和真实模型不符合，只可能是引入了噪声而已）

贝叶斯派认为：观察到的数据才是“固定”的，而我们的模型的参数才是在一直变化的。

具体到人工智能这一应用领域，基于贝叶斯定理的各种方法与人类的认知机制吻合度更高，在机器学习等领域中也扮演着更加重要的角色

估计的方法

概率估计有两种方法：最大似然估计法（maximum likelihood estimation）和最大后验概率法（maximum a posteriori estimation）

最大似然估计

体现了频率派的思想观点。

最大似然估计：使训练数据出现的概率最大化，依此确定概率分布中的未知参数，估计出的概率分布也就最符合训练数据的分布

此方法只需要使用训练数据

最大后验概率

体现了贝叶斯派的思想观念

根据训练数据和已知的其他条件，使未知参数出现的可能性最大化，并选取最可能的未知参数取值作为估计值

此方法除了训练数据外还需要先验概率

举一个例子：

一个优等生和一个差生打架，老师肯定想当然认为是差生的错，因为差生爱惹事，这就是最大似然估计；

可如果老师知道优生和差生之间原本就有过节（先验信息），把这个因素考虑进来，就不会简单地认为是差生挑衅，这就是最大后验估计。

随机变量

概率论的一个重要的应用就是描述随机变量，随机变量有两种：

  • 离散型随机变量（discrete random variable）
  • 连续型随机变量（continuous random variable）

离散变量的每个可能的取值都有大于0的概率

为了描述取值和概率之间的对应关系，对于离散型我们称为概率质量函数 probability mass function；对于连续型我们称为概率密度函数 probability density function

注意：对于连续型随机变量的概率密度函数来说，并非其真实概率，而是不同取值之间的相对关系

因为连续函数有无穷个取值，将1分配到每一个取值上面，约为0，概率密度函数的意义在于，虽然他们都为零但是也有相对关系

比如1/x与2/x，虽然x->∞均为0，但后者永远是前者的两倍

如果我们想求它的具体概率，需要在一个区间内内对其进行积分

重要的分布及他们对应的概率质量/密度函数

离散分布

两点分布：用于随机试验的结果是二进制的情形

事件发生 / 不发生的概率分别为 p/(1−p)

比如抛硬币就是典型的两点分布

二项分布：将满足参数为 p 的两点分布的随机试验独立重复 n 次

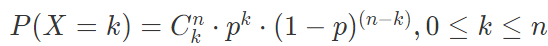
二项分布公式

  • X表示事件，k表示第几次，共n次
  • （国外Cnk 与国内Ckn书写相反，理解意思即可）
  • C表示排列组合，在n个中拿出k个的种类数

比如多次抛掷硬币，如果抛掷两次，那么就有正正、反反、正反、反正四种情况，因此公式中有排列组合C

泊松分布：放射性物质在规定时间内释放出的粒子数所满足的分布

通常被使用在估算在一段特定时间/空间内发生成功事件的数量的概率

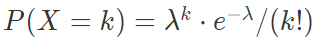
泊松分布公式

  • λ表示在一段空间/时间内事件发生的平均值
  • k表示事件发生的次数
  • e为自然常量
  • 当二项分布中的n很大且p很小时，其概率值可以由参数为 λ=np 的泊松分布的概率值近似

在Java中，HashMap的结构由链表变为红黑树的负载因子为0.75就是根据泊松分布找一个尽量使链表的长度小于8的概率

连续分布

（连续分布的概率密度函数要记得我们上一节提到的，他们只是代表相对关系，求概率需要对其积分）

均匀分布：在区间 (a, b) 上满足均匀分布的连续型随机变量，其概率密度函数为 1/(b-a)

均匀分布中，等长度概率相同

指数分布：通常用于解决表示独立随机事件发生的时间间隔（或者说，发生某事件需要多长时间）

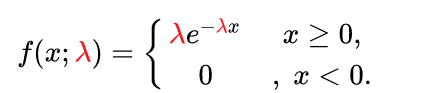
指数分布公式

  • 指数分布的一个重要特征是无记忆性：即 P(X > s + t | X > s) = P(X > t)（这个式子就可以看出与s其实没有关系，t秒之前的概率与t秒之后的概率无关）
  • 比如客服接电话，假设5秒能接一个客户，那么他半个小时后，或是一个小时后还是需要等5s才能接一个客户，也就是说，过去的实验不影响未来事件发生的概率

正态分布：自然界最常见的一种分布

正态分布公式

  • 当μ=0, σ=1为标准正态分布

数学期望、方差、协方差

描述随机变量除了函数外，还有刻画他们某些特性的常数：

  • 数学期望 expected value：即均值
  • 方差 variance：表示不同变量与期望的偏离程度。越小表示随机变量越趋近于期望，反之亦然。
  • 协方差 covariance：期望和方差都是描述单个随机变量，而协方差描述两个变量之间的关系

协方差度量了两个随机变量之间的线性相关性，即变量 Y 能否表示成以另一个变量 X 为自变量的 aX+b 的形式

协方差可以求出相关系数

相关系数是一个绝对值不大于 1 的常数：

  • =1 意味着两个随机变量满足完全正相关
  • =-1 意味着两者满足完全负相关
  • =0 意味着两者不相关

注意：协方差和相关系数只能刻画线性相关的关系，对于Y=X^2这种非线性关系无法表达