线性代数概念深入理解
线性代数概念深入理解
标量、向量、矩阵、张量
在AI中最最基础的概念。
在线性代数中,他们的概念如下
- 标量 Scalar:单独的数,如
a - 向量 Vector:多个数按一定序列排列,如
(a1,a2,a3) - 矩阵 Matrix:将向量中的每一个标量都变为一个向量,如
[(a1,a2,a3),(a4,a5,a6),(a7,a8,a9)] - 张量 Tensor:将矩阵中的每一个标量都变为一个矩阵,即一个多维矩阵
从标量到张量的过程,就是一个升高维度的过程,标量是0维,向量是一维,矩阵是二维,张量就是n维
(可以类比为点、线、面、三维立体)
在计算机存储中,标量占据的是零维数组;向量占据的是一维数组,例如语音信号;矩阵占据的是二维数组,例如灰度图像;张量占据的是三维乃至更高维度的数组,例如 RGB 图像和视频。
范数与内积
向量是虚构的概念,为了描述这些向量,提出了特定的数学语言范数和内积来描述向量的一些性质。
范数 norm
可以将一个向量映射为一个非负的数值
范数用来度量单个向量
通常用L^p来表示,公式为:
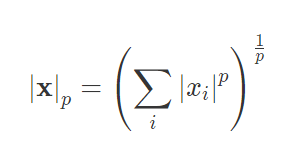
可以推得:
p=1:范数为向量的绝对值之和p=2:范数为向量的平方和再开根,通常意义上这为向量的长度(比如在二维直角坐标系中,求一个点到原点的距离就是平方求和再开根)p=∞:范数为求向量的最大的绝对值(当p无限趋近于无穷时,可以推到得其为最大的绝对值)p=-∞:范数为最小的绝对值
为什么无穷范数是最大或最小的绝对值?
看这篇文章,推导的很详细,自己复刻一遍,加深印象
内积 inner product
内积用来表示两个向量之间的关系
两个相同维数向量内积的表达式为:对应元素乘积的求和
⟨x,y⟩=∑ xi⋅yi
当内积为0时是一种特殊情况,在二维空间下,表示两个向量垂直,如(1,0)与(0,1),他们的内积是0,在二维直角坐标系下,他们也是垂直的。在更高维度下,内积为零代表正交
而且如果两个向量正交,说明他们线性无关,相互独立,互不影响。
线性空间
线性空间linear space是这样的一个集合:
- 所有向量的维度相同
- 定义了数乘、加法等结构化运算
- 如果还定义了内积运算,那么就叫内积空间 inner product space
在线性空间中:
任意一个向量代表的都是 n 维空间中的一个点;反过来, 空间中的任意点也都可以唯一地用一个向量表示。两者相互等效。
正交基
为什么要有正交基?
在现实生活中,只要给定经度、纬度和海拔高度,就可以唯一地确定地球上的任何一个位置;
但是在直觉无法感受的高维空间中,坐标系的定义可就没有这么直观了。
在内积空间中,一组两两正交的向量构成这个空间的正交基(orthogonal basis)
并且如果他们的L2范数都是单位长度1,那么这两个向量就是标准正交基
正交基就相当于给我们无法直观感受到的空间,加了一个经纬度,便于我们感受
线性空间会发生变化
一个人可以从美国去到中国,亦或反之。
在线性空间中,当确定标准正交基后,空间中的点就可以使用向量表示
当这个点从一个位置移动到另一个位置,描述他的向量也会发生变化,矩阵就是为了描述这种变化
(by the way,现在是2022年8月27日23:58:20,这直接拓宽了我的视野,这很令人兴奋)
变化可以理解为有两种:
- 点本身的变化
- 参考系的变化
因此,对于理解下面这个常见的线代式子,我们有了另一种角度
1 | Ax = y |
既可以理解为,向量x经过矩阵A变换为了y;也可以理解为,一个对象在坐标系为矩阵A时,结果为x,而在标准坐标系(单位矩阵:一个对角线为1,其余为0的矩阵)下为y
表达式Ax就相当于对向量x 做了一个环境声明,用于度量它的参考系是A。如果想用其他的参考系做度量的话,就要重新声明。
而对坐标系施加变换的方法,就是让表示原始坐标系的矩阵与表示变换的矩阵相乘。
特征值与特征向量
如上面我们提到的:让一个坐标发生变化,就是让表示原始坐标系的矩阵与表示变换的矩阵相乘。
1 | Ax=λx |
如前面所述,矩阵代表了向量的变换,其效果通常是对原始向量同时施加方向变化和尺度变化
当只有尺度变化,而没有方向变化时(或者说这个矩阵只有伸缩,没有旋转),这类特殊的向量就是矩阵的特征向量 eigenvector,特征向量的尺度变化系数就是特征值eigenvalue。
如果把矩阵所代表的变化看作奔跑的人,那么矩阵的特征值就代表了他奔跑的速度,特征向量代表了他奔跑的方向。
但矩阵可不是普通人,它是三头六臂的哪吒,他的不同分身以不同速度(特征值)在不同方向(特征向量)上奔跑,所有分身的运动叠加在⼀起才是矩阵的效果。
求解给定矩阵的特征值和特征向量的过程叫做特征值分解,但能够进行特征值分解的矩阵必须是 n 维方阵。
将特征值分解算法推广到所有矩阵之上,就是更加通用的奇异值分解。
总结
容易理解错误的点,这里再次强调一下:
- 向量是线性空间中的一个静止点
- 向量的变化(线性变换)可以看做是点的变换,也可以看做是参考系的变化,可以用矩阵表示
- 矩阵的特征值和特征向量描述了变化的速度与方向