字符串KMP算法

发表于 更新于 分类于 阅读次数： 本文字数： 1.7k 阅读时长 ≈ 2 分钟
引言：

K、M、P是三位科学家，他们以自己的首字母命名了这种字符串查找法

字符串KMP算法

适用情况

假设有字符串S，想要在其中查找字符串P，如果使用双指针去遍历，那么他的时间复杂度为O(m*n)，其中m和n为各自的字符串长度。

但是使用KMP算法，就可以压缩到O(m+n)

KMP算法

KMP算法的核心，是一个被称为部分匹配表(PMT Partial Match Table)的数组

PMT中的值是字符串的前缀集合与后缀集合的交集中最长元素的长度。

什么是PMT数组？

首先我们需要知道什么是字符串的前缀和后缀？

比如对于字符串hello来说：

  • 前缀集合：{h, he, hel, hell}
  • 后缀集合：{o, lo, llo, ello}

又比如对于字符串ababa来说：

  • 前缀集合：{a, ab, aba, abab}

  • 后缀集合：baba, aba, ba ,a}

前缀集合与后缀集合的交集为{aba, a}，最长的长度就是3了，因此我们可以对字符串ababa构造出一个数组PMT

1
2
3
4
5
6
7
str = "ababa";
pmt = {0, 0, 1, 2, 3};
// pmt[0]代表字符串"a"的前后缀交集的最长的长度
// pmt[1]代表字符串"ab"
// pmt[2]代表"aba" 
// pmt[3]代表"abab"
// pmt[4]代表"ababa"

KMP算法如何提高查询速度？

现在假设我们要在主字符串"ababababca"中查找模式字符串"abababca"

1
2
S = "ababababca";
P = "abababca";

可以根据字符串P求出PMT数组为

1
pmt = {0, 0, 1, 2, 3, 4, 0, 1};

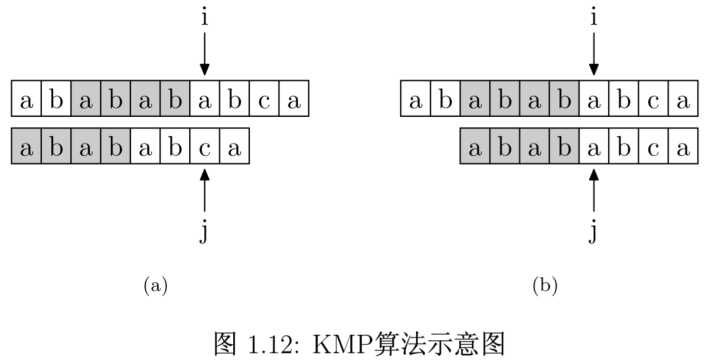
现在我们开始从S中找P，设i,j分别是S和P的指针，从0开始相互匹配，那么当出现如图(a)所示的情况时，会匹配失败，此时i,j为6

PMT[j-1]的值4，那么说明字符串S的后缀abab与字符串P的前缀abab相同

因此下一次循环，i指针无需动，j=pmt[j-1]即可，如图(b)

KMP算法演示图

Next数组

为了编程的方便，将PMT数组向前挪动1位，最开始的位置补一个-1（这个值为多少都可以，无所谓），如图所示：

next数组

Code部分

KMP的代码可以背下来，可以作为我们的一个API进行调用！！

（注意这里的next数组其实是pmt数组，并没有移动一位）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
public int strStr(String s, String p) {
    int n = s.length(), m = p.length();
    if (m == 0) return 0;

    // 使用p字符串构造Next数组
    int[] next = new int[m];
    for (int i = 1, j = 0; i < m; i++) { // i为next指针，因此初始值为1
        while (j > 0 && p.charAt(i) != p.charAt(j)) j = next[j - 1];
        if (p.charAt(i) == p.charAt(j)) j++;
        next[i] = j;
    }

    // 快速匹配
    for (int i = 0, j = 0; i < n; i++) {
        while (j > 0 && s.charAt(i) != p.charAt(j)) j = next[j - 1];
        if (s.charAt(i) == p.charAt(j)) j++;
        if (j == m) return i - m + 1;
    }
    return -1;
}

记忆点：

  • 两个循环，一个构造next，一个快速匹配
  • 第一个循环初始值i=1,j=0，是字符串p和自身比较，最后需要赋值next[i]=j
  • 第二个循环初始值i=0, j=0，是字符串s和p比较，当j==m就可以返回值了

参考资料