字符串子序列问题

发表于 更新于 分类于 阅读次数： 本文字数： 1.8k 阅读时长 ≈ 2 分钟
经典的字符串子序列问题，学习DP的第一步

字符串子序列问题

力扣字符串序列问题

首先明确几个知识点

字符串的子序列和子串不一样：

  • 子序列只要求顺序，不要求连续
  • 而子串要求顺序且要连续

比如字符串abcdefg

  • 子序列：abc、ade、acfg
  • 子串：abc、a

对于子序列问题，解法有双指针、动态规划等等解法。本文主要介绍动态规划DP这种方法

LCS问题

最长公共子序列问题是一道经典的DP问题。

动态规划方法，通常要找边界与递推式

假设字符串：

1
2
s1 = "[XXXXXXX]A"; // 假设X为未知部分，最后一个字符为A
s2 = "[XXXXXXXXX]A"; // 最后一个字符也为A

假设dp[i][j]存放了S1和S2的最长公共序列（i与j是分别指向两个字符串的指针）

​ 那么对于最后一个字符来说，他们如果相等（如S1、S2），那么此时的最长序列就是dp[i-1][j-1]+1；如果他们不相等，那么要么是在dp[i-1][j]内，要不在dp[i][j-1]内

因此我们可以得到递推式

1
2
dp[i][j] = dp[i-1][j-1]+1; // 当 s1.charAt(i) == s2.charAt(j)
dp[i][j] = Math.max(dp[i][j-1], dp[i-1][j]); // 当 s1.charAt(i) != s2.charAt(j)

此处贴一下code：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
public int longestCommonSubsequence(String text1, String text2) {
    int m = text1.length();
    int n = text2.length();

    int [][] dp = new int[m+1][n+1];

    for(int i=1; i<=m; i++){
        for(int j=1; j<=n; j++){
            if(text1.charAt(i-1) == text2.charAt(j-1)){
                dp[i][j] = dp[i-1][j-1]+1;
            }else{
                dp[i][j] = Math.max(dp[i-1][j], dp[i][j-1]);
            }
        }
    }

    return dp[m][n];
}

判断子序列

判断子序列，可以有多种求法，比如双指针就可以快速的判断，但是可以看到进阶的要求，如果出现10亿级别的数据字符串，双指针效率会很低下

这种DP可以看官方题解的视频进行理解

此处简单介绍一下：

原理相当于创建了26个字母的列表，分别记录字符串中该字母第一次出现的位置，如图

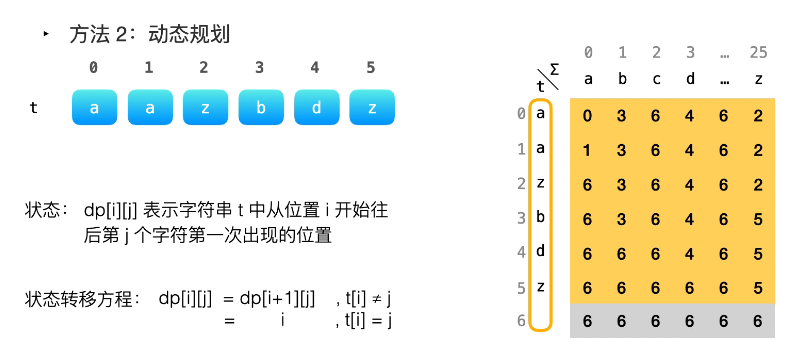
动态规划方法

因此当我们判断一个字符串是不是该字符串的子序列，就可以从第一行开始遍历，如果该字符出现过，那么就是一个小于原字符串长度的数，如果不存在那么就是字符串的长度

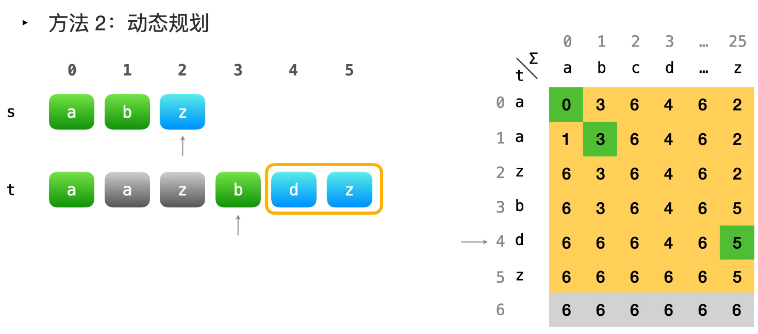
判断是否是子序列

如图所示：

  1. 首先找dp[0][s.charAt(0)-'a']，发现为0，说明存在，且下一个去找0+1
  2. 找dp[1][s.charAt(1)-'a']，发现为3，说明存在，继续找下一个3+1
  3. 找dp[4][s.charAt(2)-'a']，发现为5，说明存在，此时已经找完

贴出code：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
    public boolean isSubsequence(String s, String t) {
        int n = s.length(), m = t.length();

        int[][] f = new int[m + 1][26];
        for (int i = 0; i < 26; i++) f[m][i] = m;
        
        for (int i = m - 1; i >= 0; i--) {
            for (int j = 0; j < 26; j++) {
                if (t.charAt(i) == j + 'a')
                    f[i][j] = i;
                else
                    f[i][j] = f[i + 1][j];
            }
        }
        int add = 0;
        for (int i = 0; i < n; i++) {
            if (f[add][s.charAt(i) - 'a'] == m) 
                return false;
            add = f[add][s.charAt(i) - 'a'] + 1;
        }
        return true;
    }
}