引言:数据结构——Tire字典树
Trie 字典树
Trie
一个便于搜索的多叉树。
我们学习了树结构实现映射,它的时间复杂度是O(log n),如果有两百万个条目,大约会花费20
但是Tire查询每个条目的时间复杂度和字典中一共有多少条目无关,取决于查询单词的长度O(w)
一棵Trie就像是这样
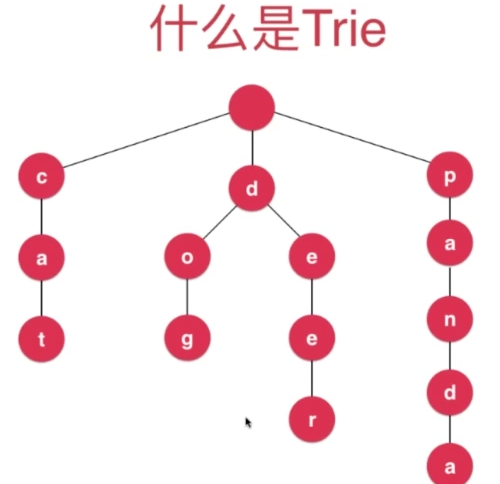
那么这样的一棵树,它的节点是如何定义的?
1
2
3
4
5
6
7
8
9
| class Node{
char c;
Node next[];
public Node(char c) {
this.c = c;
this.next = new Node[26];
}
}
|
假如我们的业务是实现单词的存储,那么应该就是这样,每一个结点可以存储26个字母。
但是假如我们的业务是存储网址信息等等,我们会扩展到更多更多,所以我们可以使用一个Map集合来充当这里的数据
1
2
3
| class Node{
Map<Character, Node> next;
}
|
但是,如果要存储单词的话,我们会遇到一个问题,就是假设存储cat和category,两个词前面都是cat,那么我们如何存储呢?
我们可以再给Node加一个字段,就是isWord
1
2
3
4
| class Node{
boolean isWord;
Map<Character, Node> next;
}
|
全部代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
| package Trie;
import java.util.Map;
import java.util.TreeMap;
public class Trie{
private class Node{
boolean isWord;
Map<Character, Node> next;
public Node(boolean isWord) {
this.isWord = isWord;
this.next = new TreeMap<>();
}
public Node(){
this(false);
}
}
private Node root;
private int size;
public Trie(){
root = new Node();
size =0;
}
public int getSize(){
return size;
}
public void add(String word){
Node cur = root;
char[] chars = word.toCharArray();
for (int i = 0; i < chars.length; i++) {
if(cur.next.get(chars[i]) == null){
cur.next.put(chars[i], new Node());
}
cur = cur.next.get(chars[i]);
}
if(!cur.isWord){
cur.isWord = true;
size ++;
}
}
public boolean contains(String word){
Node cur = root;
char[] chars = word.toCharArray();
for (int i = 0; i < chars.length; i++) {
if(cur.next.get(chars[i]) == null){
return false;
}
cur = cur.next.get(chars[i]);
}
return cur.isWord;
}
public boolean isPrefix(String prefix){
Node cur = root;
char[] chars = prefix.toCharArray();
for (int i = 0; i < chars.length; i++) {
if(cur.next.get(chars[i]) == null){
return false;
}
cur = cur.next.get(chars[i]);
}
return true;
}
}
|
