并查集

发表于 更新于 分类于 ， 阅读次数： 本文字数： 5.2k 阅读时长 ≈ 5 分钟
引言：数据结构——并查集

并查集

并查集

一种由孩子节点指向父亲节点的特殊的数据结构，可以用来很方便的解决连接问题（判断是否相互连接，如网络（社交网络）中节点间的连接状态，例如一个人是否可以通过朋友的朋友认识另一个人）

并查集主要支持两个操作：

  • union(p,q)将p和q联系起来
  • isConnected(p,q)判断p与q是否有联系

并查集接口如下：

1
2
3
4
5
public interface UnionFind {
    void union(int p, int q);
    boolean isConnected(int p, int q);
    int getSize();
}

实现

这里准备了6种实现方式，有着不同的机制或者是对方法的优化

quick find

这种实现方式使得我们isConnected方法更快（O(1)级别），但是union方法会比较慢

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
/**
 * @Date 2020/9/26 10:52
 * quick find
 */
public class UnionFind1 implements UnionFind {

    // 表示数据的下标，可以理解为一个指针
    private int[] id;
    

    public UnionFind1(int size) {
        this.id = new int[size];
        // 给每一个数据一个不同的下标
        for (int i = 0; i < id.length; i++) {
            id[i] = i;
        }
    }

    /**
     * 合并元素p和元素q所属的集合
     * @param p
     * @param q
     */
    @Override
    public void union(int p, int q) {
        int pId = find(p);
        int qId = find(q);
        if(pId == qId) {
            return;
        } else {
            for (int i = 0; i < id.length; i++) {
                if(id[i] == pId) {
                    id[i] = qId;
                }
            }
        }
    }

    /**
     * 查看元素p和q是否在一个集合
     * @param p
     * @param q
     * @return
     */
    @Override
    public boolean isConnected(int p, int q) {
        return find(p) == find(q);
    }

    /**
     * 查找元素p所对应的集合编号
     * @param p
     * @return
     */
    private int find(int p){
        if(p<0&&p>=id.length) {
            throw new IllegalArgumentException("不正确的下标");
        }
        return id[p];
    }
    @Override
    public int getSize() {
        return id.length;
    }
}

quick union

主流的并查集的实现方式，将两个操作的时间复杂度都为O(h)，h为树的高度

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
/**
 * @Date 2020/9/26 11:06
 * quick union
 */
public class UnionFind2 implements UnionFind {

    private int[] parent;
    public UnionFind2(int size){
        parent = new int[size];
        for (int i = 0; i < parent.length; i++) {
            parent[i] = i;
        }
    }

    @Override
    public void union(int p, int q) {
        int pRoot = find(p);
        int qRoot = find(q);
        if(pRoot == qRoot){
            return;
        }
        parent[pRoot] = qRoot;
    }

    @Override
    public boolean isConnected(int p, int q){
        return find(p) == find(q);
    }

    /**
     * 找到对应的根节点
     * @param p
     * @return
     */
    private int find(int p){
        if(p<0&&p>=parent.length) {
            throw new IllegalArgumentException("不正确的下标");
        }
        while (p!=parent[p]){
            p = parent[p];
        }
        return p;
    }

    @Override
    public int getSize() {
        return parent.length;
    }
}

优化Union

增加了一个字段sz，存储以i为根的集合中元素的个数，在Union操作的时候，我们可以将元素个数少的指向元素个数多的

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
/**
 * @Date 2020/9/26 15:04
 */
public class UnionFind3 implements UnionFind{

    private int[] parent;
    private int[] sz;   // 以i为根的集合中元素的个数

    public UnionFind3(int size){
        parent = new int[size];
        sz = new int[size];
        for (int i = 0; i < parent.length; i++) {
            parent[i] = i;
            sz[i] = 1;
        }
    }

    @Override
    public void union(int p, int q) {
        int pRoot = find(p);
        int qRoot = find(q);
        if(pRoot == qRoot){
            return;
        }
        // -----------------这里-----------------------
        // 将元素少的合并到元素多的元素上
        if(sz[pRoot] > sz[qRoot]){
            parent[pRoot] = qRoot;
            sz[qRoot]+= sz[pRoot];
        }else {
            parent[qRoot] = pRoot;
            sz[pRoot] += sz[qRoot];
        }

    }

    @Override
    public boolean isConnected(int p, int q){
        return find(p) == find(q);
    }

    /**
     * 找到对应的根节点
     * @param p
     * @return
     */
    private int find(int p){
        if(p<0&&p>=parent.length) {
            throw new IllegalArgumentException("不正确的下标");
        }
        while (p!=parent[p]){
            p = parent[p];
        }
        return p;
    }

    @Override
    public int getSize() {
        return parent.length;
    }
}

优化为rank

其实我们可以直接存储树的高度，而不是元素的个数，如图

image-20200926171718329 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65

/**
 * @Date 2020/9/26 15:14
 * rank优化
 */
public class UnionFind4 implements UnionFind {

    private int[] parent;
    private int[] rank;   // 以i为根的集合所表示的树的高度

    public UnionFind4(int size) {
        parent = new int[size];
        rank = new int[size];
        for (int i = 0; i < parent.length; i++) {
            parent[i] = i;
            rank[i] = 1;
        }
    }

    @Override
    public void union(int p, int q) {
        int pRoot = find(p);
        int qRoot = find(q);
        if (pRoot == qRoot) {
            return;
        }
        // 将树高更低的集合合并到高的集合上
        if (rank[pRoot] < rank[qRoot]) {
            parent[pRoot] = qRoot;
        } else if (rank[pRoot] > rank[qRoot]){
            parent[qRoot] = pRoot;
        }else {// 相等情况
            parent[qRoot] = pRoot;
            rank[qRoot]++;
        }

    }

    @Override
    public boolean isConnected(int p, int q) {
        return find(p) == find(q);
    }

    /**
     * 找到对应的根节点
     *
     * @param p
     * @return
     */
    private int find(int p) {
        if (p < 0 && p >= parent.length) {
            throw new IllegalArgumentException("不正确的下标");
        }
        while (p != parent[p]) {
            p = parent[p];
        }
        return p;
    }

    @Override
    public int getSize() {
        return parent.length;
    }
}

路径压缩

一个并查集，我们主要实现的操作就是两个，但是在极端情况下，我们发现还是会出现树很高的现象，但其实

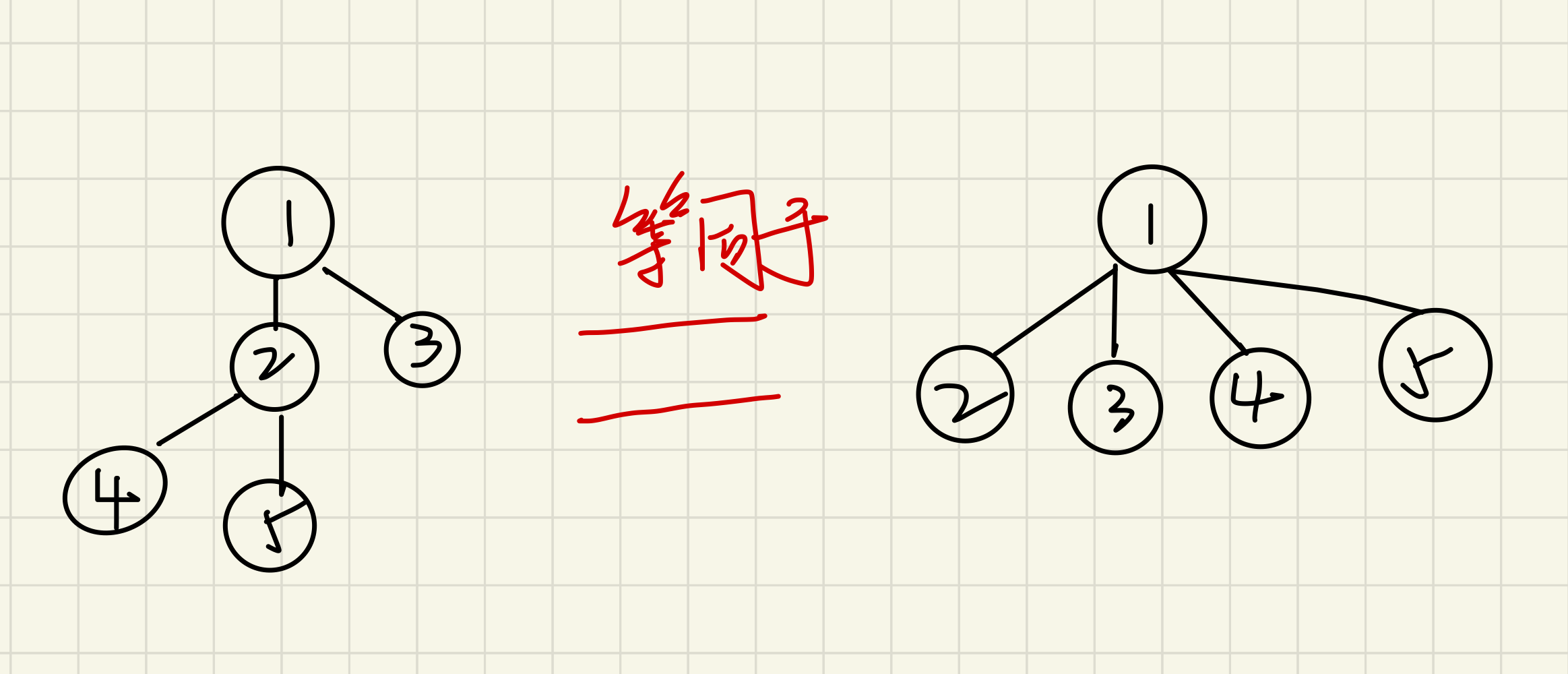
792B641FCB4938C17D652E612E2B58F2

只需要优化一下find方法，我们就可以在每次find时，更改树的结构

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
/**
 * 找到对应的根节点
 *
 * @param p
 * @return
 */
private int find(int p) {
    if (p < 0 && p >= parent.length) {
        throw new IllegalArgumentException("不正确的下标");
    }
    while (p != parent[p]) {
        // 就是这一行代码
        parent[p] = parent[parent[p]];
        p = parent[p];
    }
    return p;
}

这一行代码：parent[p] = parent[parent[p]];看上去很复杂，其实就是在遍历到这里时，把该节点的父节点 换成父节点的父节点

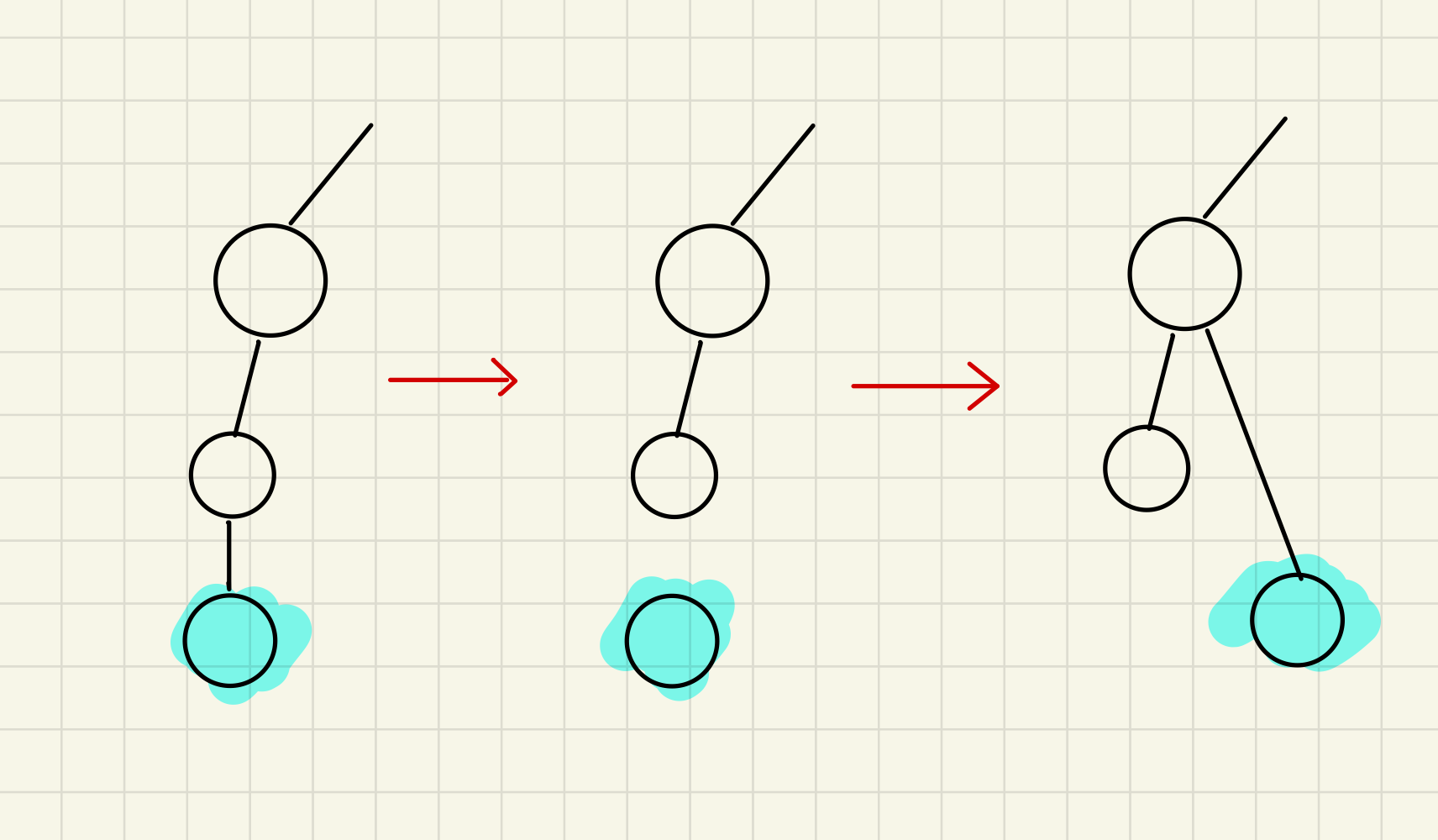
image-20200926173332231

每一次find，我们都可以优化一遍，最后所有的子节点都会指向一个根，这样我们的树高大大的降低，这种路径压缩的操作，最后会

递归优化

经过路径优化后，你可能在想，为什么不直接在第一次find的时候，就将子节点连接到根节点呢？

所以我们可以这样优化

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
/**
 * 找到对应的根节点
 *
 * @param p
 * @return
 */
private int find(int p) {
    if (p < 0 && p >= parent.length) {
        throw new IllegalArgumentException("不正确的下标");
    }
    if (p != parent[p]) {
        parent[p] = find(parent[p]);
    }
    return parent[p];
}

时间复杂度分析

经过优化后，并查集的时间复杂度为*O(logn)**（推导十分复杂）

image-20200926153651479