堆和优先队列

发表于 更新于 分类于 ， ， 阅读次数： 本文字数： 3.5k 阅读时长 ≈ 3 分钟
引言：数据结构——优先队列和堆

堆和优先队列

优先队列

  • 普通队列：先进先出FIFO

  • 优先队列：出队顺序和入队顺序无关，和优先级相关

优先队列应用很广，比如操作系统的任务调度，就需要动态选择优先级最高的任务执行；还有一个游戏的AI，当敌人来了之后会默认的攻击威胁程度最大的敌人等等，都使用了优先队列

优先队列需要实现的接口依然还是

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

/**
 * @author BlackKnight
 */
public interface Queue<E> {
    int getSize();
    boolean isEmpty();

    /**
     *入队列
     * @param e
     */
    void enqueue(E e);
    /**
     * 出队列
     * @return
     */
    E dequeue();

    /**
     * 得到队头元素
     * @return
     */
    E getFront();
}

但是我们可以使用不用的数据结构实现相同的功能，比如说普通的线性结构（数组，链表），比如说顺序的线性结构（保持着排序）等等，但是最好的方式是使用堆来实现，比较如下

image-20200923193815224

二叉堆

二叉堆是一棵完全二叉树（缺失的叶子节点都在右下方）

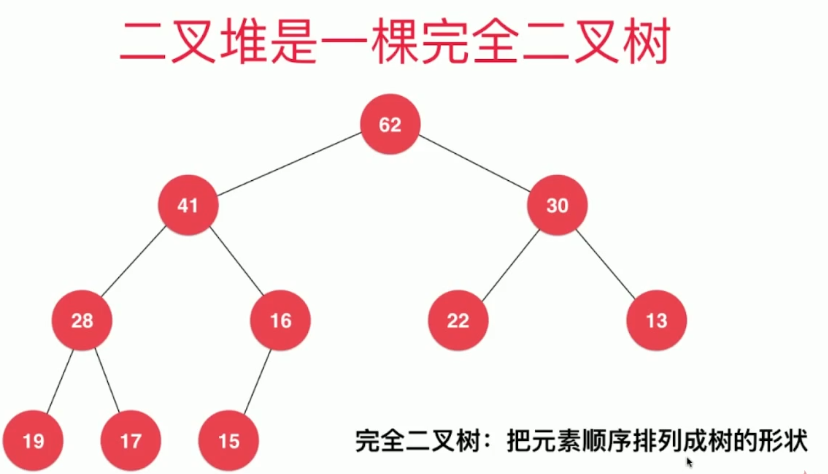
image-20200923194406290

堆的特性：

  • 一棵完全二叉树
  • 一颗平衡二叉树
  • 堆的某个节点的值总是不大于其父节点的值（最大堆）
  • 同上也有最小堆

可以使用树的结构来实现堆，但是由于堆是一棵完全二叉树，所以可以使用数组来实现完全二叉树（可以完美的对应数组的下标）

image-20200923195338585

如图，有三条性质，这三条性质就是数组下标和二叉堆结点的对应关系，而且为了防止0号空间无使用，我们略微改变了一下，就有

  • parent(i) = ( i - 1 ) / 2
  • leftChild (i) = 2*i +1
  • rightChild (i) = 2*i + 2

使用数组实现二叉堆，代码如下：（数组使用我们之前实现的数组）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
import array.Array;

/**
 * @Date 2020/9/23 20:35
 * 最大堆
 */
public class MaxHeap<E extends Comparable<E>> {
    /**
     * 使用数组实现堆
     */
    private Array<E> data;

    public MaxHeap(int capacity) {
        data = new Array<>(capacity);
    }

    public MaxHeap() {
        data = new Array<>();
    }

    /**
     * 返回堆中的元素个数
     *
     * @return
     */
    public int size() {
        return data.getSize();
    }

    /**
     * 返回一个布尔值，表示堆是否为空
     *
     * @return
     */
    public boolean isEmpty() {
        return data.isEmpty();
    }

    /**
     * 三个辅助方法：
     * 1. 返回完全二叉树的数组表示中，一个索引所表示的元素的父亲节点的索引
     */
    private int parent(int index) {
        if (index == 0) {
            throw new IllegalArgumentException("索引0：没有父亲节点");
        }
        return (index - 1) / 2;
    }

    /**
     * 三个辅助方法：
     * 2. 返回完全二叉树的数组表示中，一个索引所表示的元素的左孩子节点的索引
     */
    private int leftChild(int index) {
        return 2 * index + 1;
    }

    /**
     * 三个辅助方法：
     * 3. 返回完全二叉树的数组表示中，一个索引所表示的元素的右孩子节点的索引
     */
    private int rightChild(int index) {
        return 2 * index + 2;
    }

    /**
     * 向堆中添加元素
     */
    public void add(E e) {
        data.addLast(e);
        siftUp(data.getSize() - 1);
    }

    /**
     * 调整最大堆的结构
     *
     * @param k 传入索引
     */
    private void siftUp(int k) {
        while (k > 0 && data.get(parent(k)).compareTo(data.get(k)) < 0) {
            // 交换两个元素
            swap(k, parent(k));
            k = parent(k);
        }
    }

    private void swap(int i, int j) {
        E temp = data.get(i);
        data.set(i, data.get(j));
        data.set(j, temp);
    }

    public E findMax() {
        if (isEmpty()) {
            throw new IllegalArgumentException("堆是空的");
        }
        return data.get(0);
    }

    public E extractMax() {
        E e = findMax();
        // 先将最大和最小交换位置
        swap(0, data.getSize() - 1);
        // 删除最后一个元素
        data.removeLast();
        siftDown(0);
        return e;
    }

    private void siftDown(int k) {
        // 如果左孩子都越界了，那么肯定要停止了
        while (leftChild(k) < data.getSize()) {
            int j = leftChild(k);
            // 判断有没有右孩子，且 右孩子比左孩子大
            if (j + 1 < data.getSize()
                    && data.get(j + 1).compareTo(data.get(j)) > 0) {
                j++;
                // data.get(j) 是左右孩子中的最大值
            }
            // 如果 k位置的值比他的两个孩子内更大的孩子大，说明已经完成调度
            if (data.get(k).compareTo(data.get(j)) >= 0) {
                break;
            }
            swap(k, j);
            k = j;
        }
    }

}

关于增添方法和删除方法

增添方法思想：

将要添加的元素放在完全二叉树的最后一个节点，然后逐级与根节点比较，放置在一个合适的位置上

删除方法思想：

交换堆顶和最后一个节点，将新的头结点放置在一个合适的位置

优先队列

有了二叉堆，实现优先队列就特别简单了

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39

package queue;

import heap.MaxHeap;

/**
 * @Date 2020/9/23 19:31
 * 优先队列
 */
public class PriorityQueue<E extends Comparable<E>> implements Queue<E>{

    private MaxHeap<E> maxHeap;

    @Override
    public int getSize() {
        return maxHeap.size();
    }

    @Override
    public boolean isEmpty() {
        return maxHeap.isEmpty();
    }

    @Override
    public void enqueue(E e) {
        maxHeap.add(e);
    }

    @Override
    public E dequeue() {
        return maxHeap.extractMax();
    }

    @Override
    public E getFront() {
        return maxHeap.findMax();
    }
}