引言:数据结构——集合Set
集合
Set
集合:
一个无序的,不会存放相同元素的特殊的数据结构。
需要实现如下方法:
1
2
3
4
5
6
7
| public interface Set<E> {
void add(E e);
void remove(E e);
boolean contains(E e);
int getSize();
boolean isEmpty();
}
|
特点:
分别使用二叉搜索树和链表来实现集合
LinkedListSet
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
| public class LinkedListSet<E> implements Set<E> {
private LinkedList<E> linkedList;
public LinkedListSet() {
linkedList = new LinkedList<>();
}
@Override
public void add(E e){
if(!linkedList.contains(e)){
linkedList.addFirst(e);
}
}
@Override
public void remove(E e) {
linkedList.removeElement(e);
}
@Override
public boolean contains(E e) {
return linkedList.contains(e);
}
@Override
public int getSize() {
return linkedList.getSize();
}
@Override
public boolean isEmpty() {
return linkedList.isEmpty();
}
}
|
BstSet
二分搜索树来实现集合
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
| public class BstSet<E extends Comparable<E>> implements Set<E> {
private BinarySearchTree<E> bst;
public BstSet() {
bst = new BinarySearchTree<>();
}
@Override
public void add(E e) {
bst.add(e);
}
@Override
public void remove(E e) {
bst.remove(e);
}
@Override
public boolean contains(E e) {
return bst.contains(e);
}
@Override
public int getSize() {
return bst.size();
}
@Override
public boolean isEmpty() {
return bst.isEmpty();
}
}
|
复杂度分析
LinkedListSet
- 增 add:O(n)
- 查 contains:O(n)
- 删 remove: O(n)
BstSet
最多访问树的高度 h
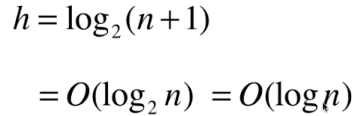
- 增 add :O(log n)
- 查 contains:O(log n)
- 删 remove: O(log n)
结论
二叉搜索树实现的集合要比链表实现的集合性能高的多。
但是当存储的数据为顺序的话,二叉搜索树有可能是这个样子的
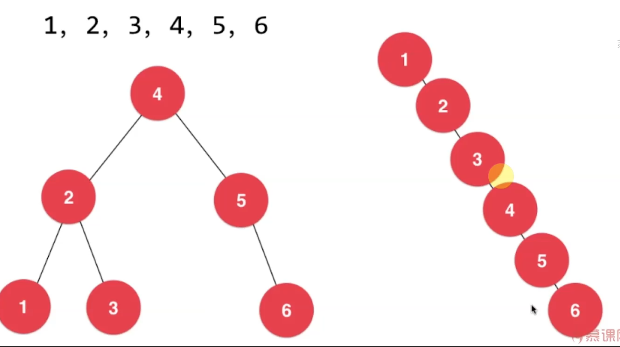
这个时候二叉搜索树的性能将会和链表一样(AVL树可以解决这种问题)。