单精度与双精度浮点数与十进制 之间的转换

发表于 更新于 分类于 阅读次数： 本文字数： 2.4k 阅读时长 ≈ 2 分钟
引言：

根据IEEE 754标准：单精度与双精度浮点数 与 十进制 之间的转换

根据IEEE 754标准：单精度与双精度浮点数 与 十进制 之间的转换

单精度与双精度

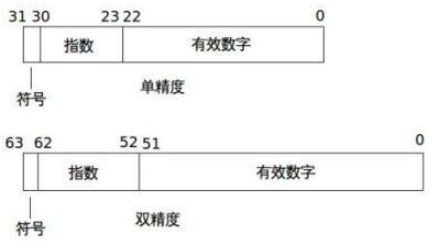
image-20200811215348594

根据IEEE 754 标准，单双精度有如下区别：

单精度：符号(1 bit) + 阶码(8 bit) + 尾数(23 bit) ； 偏置常量 = 127 非规格化为 126

双精度：符号(1 bit) + 阶码(11 bit) + 尾数(52 bit) ； 偏置常量 = 1023 非规格化为 1022

单精度转换为十进制数

例1：0x FF80 0000 转换为 十进制

1
2
3
4
5
6
7
ff80 0000 
转换为二进制
1111 1111 1000 0000 0000 0000 0000 0000
其中分别为符号位、阶码、还有尾数
1  | 111  1111 1 | 000 0000 0000 0000 0000 0000
由此可以看出，这个数是负数，阶码全1，尾数全0
所以这个数比较特殊，答案是：负无穷

无穷大（尾数全0，阶码全1，根据符号位又区分出无穷大和无穷小）

例2：0x 7FE0 0000 转换为 十进制

1
2
3
4
5
6
7
7fe0 0000
转换为二进制
0111 1111 1110 0000 0000 0000 0000 0000
分开
0 | 111 1111 1 | 110 0000 0000 0000 0000 0000
这是一个正数，而且阶码全1 ， 尾数非0
这又是一种特殊情况，非数

非数 NaN（阶码全1 ， 尾数非0）

例3： 0x C1C9 0000 转换为十进制

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
C1C9 0000
转换为二进制
1100 0001 1100 1001 0000 0000 0000 0000
分开
1 | 100 0001 1 | 100 1001 0000 0000 0000 0000
发现这个数是一个负数，阶码与尾数都没有什么特殊点

由于是单精度浮点型，所以将阶码减去127
	1000 0011
-    0111 1111
——————————————————
得   0000 0100  为 4

在看尾数，转换为小数为
1 + 2^-1 + 2^-4 + 2^-7 （由于是规格化非0数，1是隐含的）
= 1.5703125

此时将 2^4 * 1.5703125 = 25.125
在看符号位，所以最后的结果为
-25.125

双精度转换为十进制

例1: 0x 8008 0000 0000 0000 转换为十进制

1
2
3
4
5
6
7
同样的道理 ，转换
1000 0000 0000 1000 0000 ... 0000
分开，注意双进度阶码有11位
1 | 000 0000 0000 | 1000 0000 ... 0000
阶码全0，尾数非0，所以这是一个 非规格化非0数（所以不能减1023，要减去1022）

所以结果为 -0.5 * 2^-1022 （由于是非规格化，所以是隐含是0，而不是1）

例2: 0x 7065 0200 0000 0000 转换为十进制

1
2
3
4
5
6
7
8
9
10
11
12
13
14
7065 0200 0000 0000 
转换为二进制
0111 0000 0110 0101 0000 0010 0000 ... 0000
分开
0 | 111 0000 0110 | 0101 0000 0010 0000 ... 0000
可以看出是一个正数，而且阶码和尾数都没有什么特殊点，为规格化非0数
	111 0000 0110
- 	011 1111 1111 （1023）
——————————————————
	011 0000 0111 （775）

尾数化为小数 1 + 2^-2 + 2^-4 + 2^-11 = 1.31298828125

结果为 1.31298828125 * 2^775

十进制转换为单精度

例1: 0 转换为单精度

1
2
3
在IEEE 754 标准中
尾数全0 阶码全0 代表0
根据符号不同，有+0和-0的区别

例2: 116.25转换为单精度

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
116.25 
我们先来想，2的幂次中，小于116而且最近的一个数字
128太大，只能为64
64 为 2^6 所以阶码为 6 + 127 转换为二进制 1000 0101

现在用 116.25 / 64 = 1.81640625 
其中1隐含掉，求0.81640625的二进制0.11010001

所以结果的二进制码为
0 | 100 0010 1 | 110 1000 1000 ... 0000
也就是
0100 0010 1110 1000 1000 0000 ... 0000
所以化为16进制为
0x 42E8 0000

例3： -4.375 转化为单精度

1
2
3
4
5
6
7
8
9
10
11
12
同理，寻找与4最近的，即2^2，所以阶码就是2+127 为 1000 0001

再用4.375 / 4 = 1.09375

用二进制表示0.09375 为 0.00011

所以结果为
1 | 100 0000 1 | 000 1100 0000 ... 0000
即
1100 0000 1000 1100 0000 ... 0000
转换为16进制
C08C 0000

十进制转换为双精度

例1：116.25 转换为双精度

1
2
3
4
5
6
7
8
9
10
11
同理，寻找到64 也就是6
6+1023 转换为二进制 100 0000 0101 ，这就是阶码

现在用 116.25 / 64 = 1.81640625 转换为二进制 0.11010001

所以结果为

0 | 100 0000 0101 | 1101 0001 0000... 0000
结果就是
405D 1000 0000 ... 0000

例2：-2049.5转换为双精度

1
2
3
4
5
6
7
8
9
10
11
寻找一个距离2049最近的，也就是2048，即2的11次方
11 + 1023 转换为二进制100 0000 1010

2049.5 / 2048 = 1.000732421875
尾数转换为二进制0.000000000011

所以结果为
1 | 100 0000 1010 | 0000 0000 0011 0000 ... 0000
转换为16进制
C0A0 0030 0000 0000 ... 0000

总结

  • 注意是否为非数（NaN）或者是无穷大

    • 非数：阶码全1 尾数非0

    • 无穷大：阶码全1 尾数全0

  • 注意是否是规格化非0数

    • 规格化非0数（阶码非全1非全0），此时隐藏的尾数为1，偏置常量为127或是1023
    • 非规格化非0数（阶码全0，尾数非0），此时隐藏的尾数为0，偏置常量为126或是1022

以上就是全部啦

:wq